
【题目】高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资,已知生产每件产品的成本是40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额一生产成本—投资)为z(万元).
(1)试写出y与x之间的函数关系式(不写x的取值范围);
(2)试写出z与x之间的函数关系式(不写x的取值范围);
(3)公司计划,在第一年按年获利最大确定销售单价进行销售;到第二年年底获利不低于1130万元,请借助函数的大致图象说明:第二年的销售单价x(元)应确定在什么范围内?
【答案】(1)y=-![]() x+30;(2)z=-
x+30;(2)z=-![]() x2+34x-3200;(3)第二年的销售单价应确定在不低于120元且不高于220元的范围内.
x2+34x-3200;(3)第二年的销售单价应确定在不低于120元且不高于220元的范围内.
【解析】
试题(1)依题意当销售单价定为x元时,年销售量减少![]() (x-100),则易求y与x之间的函数关系式.
(x-100),则易求y与x之间的函数关系式.
(2)由题意易得Z与x之间的函数关系.
(3)根据z=(30-![]() x)(x-40)-310=-
x)(x-40)-310=-![]() x2+34x-1510=1130进而得出当120≤x≤220时,z≥1130画出图象得出即可.
x2+34x-1510=1130进而得出当120≤x≤220时,z≥1130画出图象得出即可.
试题解析:(1)依题意知,当销售单价定为x元时,年销售量减少![]() (x-100)万件.
(x-100)万件.
∴y=20-![]() (x-100)=-
(x-100)=-![]() x+30.
x+30.
即y与x之间的函数关系式是:y=-![]() x+30.
x+30.
(2)由题意,得:z=(30-![]() )(x-40)-500-1500=-
)(x-40)-500-1500=-![]() x2+34x-3200.
x2+34x-3200.
即z与x之间的函数关系式是:z=-![]() x2+34x-3200.
x2+34x-3200.
(3)∵z=-![]() x2+34x-3200=-
x2+34x-3200=-![]() (x-170)2-310.
(x-170)2-310.
∴当x=170时,z取最大值,最大值为-310.
也就是说:当销售单价定为170元时,年获利最大,并且到第一年底公司还差310万元就可以收回全部投资.
第二年的销售单价定为x元时,则年获利为:
z=(30-![]() x)(x-40)-310
x)(x-40)-310
=-![]() x2+34x-1510.
x2+34x-1510.
当z=1130时,即1130=-![]() +34-1510.
+34-1510.
整理,得x2-340x+26400=0.
解得x1=120,x2=220.
函数z=-![]() x2+34x-1510的图象大致如图所示:
x2+34x-1510的图象大致如图所示:
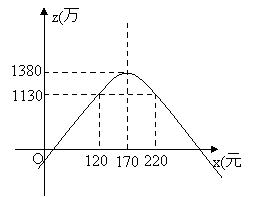
由图象可以看出:当120≤x≤220时,z≥1130.
所以第二年的销售单价应确定在不低于120元且不高于220元的范围内.
考点:二次函数的应用.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
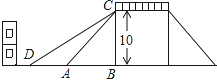
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
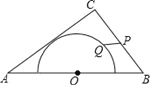
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
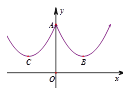
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
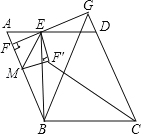
【题目】如图,平行四边形ABCD中,过点B作BE⊥AD于点E,过点E作EF⊥AB于点F,与CD的延长线交于点G,连接BG,且BE=BC,BG=5![]() ,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m-3)x+m+1经过点A(1,4)
(1)求m的值;
(2)画出此一次函数的图象;
(3)若一次函数交y轴于点B,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
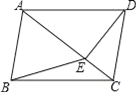
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 明德中学在商场购买甲、乙两种不同足球,购买甲种足球共花费3000元,购买乙种足球共花费2100元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)为响应国家“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2950元,那么这所学校最多可购买多少个乙种足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com