
【题目】已知![]() 为直线
为直线![]() 上的一点,
上的一点,![]() 是直角,
是直角,![]() 平分
平分![]() .
.
(1)如图1,若![]() =
=![]() °,则
°,则![]() = °,
= °,![]() 与
与![]() 的数量关系为 .
的数量关系为 .
(2)当射线![]() 绕点
绕点![]() 逆时针旋转到如图2的位置时,(1)中
逆时针旋转到如图2的位置时,(1)中![]() 与
与![]() 的关系是否仍然成立?如成立,请说明理由.
的关系是否仍然成立?如成立,请说明理由.
(3)在图3中,若![]() =
=![]() °,在
°,在![]() 的内部是否存在一条射线
的内部是否存在一条射线![]() ,使得
,使得![]() ?若存在,请求出
?若存在,请求出![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

【答案】(1)56°;∠BOE=2∠COF;(2) ∠BOE=2∠COF仍然成立,理由见解析;(3)存在,∠BOD=16°.
【解析】
(1)由题意可知:∠FOE=90°∠COF,由角平分线的性质可求得∠AOE=2∠EOF,所以∠BOE=180°∠AOE,即可求得答案,设∠COF=n°,同理可得∠BOE=2∠COF;
(2)设∠COF=n°,故∠EOF=90°n,由角平分线的性质即可求得∠AOE=180°2n°,从而求得∠BOE与∠COF的数量关系;
(3)由(2)可知:∠BOE=2∠COF=130°,进而求得∠AOE=180°∠BOE=50°,由于OF平分∠AOE,所以∠AOF=![]() ∠AOE=25°,分别代入2∠BOD+∠AOF=
∠AOE=25°,分别代入2∠BOD+∠AOF=![]() (∠BOE∠BOD)解得∠BOD即可.
(∠BOE∠BOD)解得∠BOD即可.
解:(1)∵∠COE是直角,∠COF=28°,
∴∠EOF=90°∠COF=62°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=124°,
∴∠BOE=180°∠AOE=56°,
若∠COF=n°,则∠EOF=90° n°,
∴∠AOE=2∠EOF=180° 2n°,
∴∠BOE=180°∠AOE=2n°,
∴∠BOE=2∠COF;
(2)∠BOE=2∠COF仍然成立,
理由:设∠COF=n°,
∴∠EOF=90°∠COF=90°n°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°2n°,
∴∠BOE=180°∠AOE=2n°=2∠COF,
故∠BOE与∠COF的关系是仍然成立;
(3)由(2)可知:∠BOE=2∠COF=130°,
∴∠AOE=180°∠BOE=50°,
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=25°,
∠AOE=25°,
∵2∠BOD+∠AOF=![]() (∠BOE∠BOD),
(∠BOE∠BOD),
∴2∠BOD+25°=![]() (130°∠BOD)
(130°∠BOD)
解得:∠BOD=16°.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:
【题目】如图,在同一平面内四个点A,B,C,D.
(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.
①作射线AC;
②连接AB,BC,BD,线段BD与射线AC相交于点O;
③在线段AC上作一条线段CF,使CF=AC﹣BD.
(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是 .
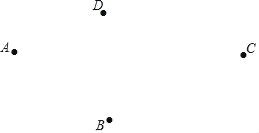
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (
(![]() 、
、![]() 是正整数,且
是正整数,且![]() ).在n的所有这种分解中,如果
).在n的所有这种分解中,如果![]() 、
、![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是n的最佳分解,并规定:
是n的最佳分解,并规定:![]() .例如12可以分解成
.例如12可以分解成![]() ,
,![]() 或
或![]() ,因为
,因为![]() ,所以
,所以![]() 是12的最佳分解,所以
是12的最佳分解,所以![]() .如果一个两位正整数
.如果一个两位正整数![]() ,
,![]() (
(![]() ,
,![]() 、
、![]() 为正整数),交换其个位上的数字与十位上的数字得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数
为正整数),交换其个位上的数字与十位上的数字得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数![]() 为“吉祥数”,则所有“吉祥数”中
为“吉祥数”,则所有“吉祥数”中![]() 的最大值为_____________.
的最大值为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用大小相等的小五角星按一定规律拼成的一组图案,第1个图案中有4颗五角星,第2个图案中有7颗五角星,第3个图案中有10颗五角星,…,请根据你的观察完成下列问题.

(1)根据上述规律,分别写出第4个图案和第5个图案中小五角星的颗数;
(2)按如图所示的规律,求出第![]() 个图案中小五角星的颗数(用含
个图案中小五角星的颗数(用含![]() 的代数式表示);
的代数式表示);
(3)求第2019个图案中小五角星的颗数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①两个数互为倒数,则它们乘积为1;②若a、b互为相反数,则![]() =﹣1;③两个四次单项式的和一定是四次多项式;④两个有理数比较,绝对值大的反而小;⑤若a为任意有理数,则a﹣|a|≤0;⑥﹣5πR2的系数是﹣5.其中正确的有( )
=﹣1;③两个四次单项式的和一定是四次多项式;④两个有理数比较,绝对值大的反而小;⑤若a为任意有理数,则a﹣|a|≤0;⑥﹣5πR2的系数是﹣5.其中正确的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
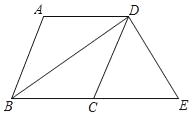
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,当图形W上的点P的横坐标和纵坐标相等时,则称点P为图形W的“梦之点”.
(1)已知⊙O的半径为1.
①在点E(1,1),F(![]() ,-
,-![]() ),M(-2,-2)中,⊙O的“梦之点”为 ;
),M(-2,-2)中,⊙O的“梦之点”为 ;
②若点P位于⊙O内部,且为双曲线![]() (k≠0)的“梦之点”,求k的取值范围.
(k≠0)的“梦之点”,求k的取值范围.
(2)已知点C的坐标为(1,t),⊙C的半径为![]() ,若在⊙C上存在“梦之点”P,直接写出t的取值范围.
,若在⊙C上存在“梦之点”P,直接写出t的取值范围.
(3)若二次函数![]() 的图象上存在两个“梦之点”
的图象上存在两个“梦之点”![]() ,
,![]() ,且
,且![]() ,求二次函数图象的顶点坐标.
,求二次函数图象的顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com