
【题目】如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.
(1)求点A的坐标;
(2)设二次函数图象的顶点为F,其对称轴与直线AB及x轴分别交于点D和点E,若△FCD与△AED相似,求此二次函数的关系式.
【答案】
(1)
解:如图,过点C作CM∥OA交y轴于M.
∵AC:BC=3:1,
∴ ![]() =
= ![]() .
.
∵CM∥OA,
∴△BCM∽△BAO,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OA=4CM=4,
∴点A的坐标为(﹣4,0);
(2)
解:∵二次函数y=ax2+bx(a<0)的图象过A点(﹣4,0),
∴16a﹣4b=0,
∴b=4a,
∴y=ax2+4ax,对称轴为直线x=﹣2,
∴F点坐标为(﹣2,﹣4a).
设直线AB的解析式为y=kx+n,将A(﹣4,0)代入,
得﹣4k+n=0,
∴n=4k,
∴直线AB的解析式为y=kx+4k,
∴B点坐标为(0,4k),D点坐标为(﹣2,2k),C点坐标为(﹣1,3k).
∵C(﹣1,3k)在抛物线y=ax2+4ax上,
∴3k=a﹣4a,
∴k=﹣a.
∵△AED中,∠AED=90°,
∴若△FCD与△AED相似,则△FCD是直角三角形,
∵∠FDC=∠ADE<90°,∠CFD<90°,
∴∠FCD=90°,
∴△FCD∽△AED.
∵F(﹣2,﹣4a),C(﹣1,3k),D(﹣2,2k),k=﹣a,
∴FC2=(﹣1+2)2+(3k+4a)2=1+a2,CD2=(﹣2+1)2+(2k﹣3k)2=1+a2,
∴FC=CD,
∴△FCD是等腰直角三角形,
∴△AED是等腰直角三角形,
∴∠DAE=45°,
∴∠OBA=45°,
∴OB=OA=4,
∴4k=4,
∴k=1,
∴a=﹣1,
∴此二次函数的关系式为y=﹣x2﹣4x.
【解析】(1)过点C作CM∥OA交y轴于M,则△BCM∽△BAO,根据相似三角形对应边成比例得出 ![]() =
= ![]() ,即OA=4CM=4,由此得出点A的坐标为(﹣4,0);(2)先将A(﹣4,0)代入y=ax2+bx,化简得出b=4a,即y=ax2+4ax,则顶点F(﹣2,﹣4a),设直线AB的解析式为y=kx+n,将A(﹣4,0)代入,化简得n=4k,即直线AB的解析式为y=kx+4k,则B点(0,4k),D(﹣2,2k),C(﹣1,3k).由C(﹣1,3k)在抛物线y=ax2+4ax上,得出3k=a﹣4a,化简得到k=﹣a.再由△FCD与直角△AED相似,则△FCD是直角三角形,又∠FDC=∠ADE<90°,∠CFD<90°,得出∠FCD=90°,△FCD∽△AED.再根据两点之间的距离公式得出FC2=CD2=1+a2 , 得出△FCD是等腰直角三角形,则△AED也是等腰直角三角形,所以∠DAE=45°,由三角形内角和定理求出∠OBA=45°,那么OB=OA=4,即4k=4,求出k=1,a=﹣1,进而得到此二次函数的关系式为y=﹣x2﹣4x.
,即OA=4CM=4,由此得出点A的坐标为(﹣4,0);(2)先将A(﹣4,0)代入y=ax2+bx,化简得出b=4a,即y=ax2+4ax,则顶点F(﹣2,﹣4a),设直线AB的解析式为y=kx+n,将A(﹣4,0)代入,化简得n=4k,即直线AB的解析式为y=kx+4k,则B点(0,4k),D(﹣2,2k),C(﹣1,3k).由C(﹣1,3k)在抛物线y=ax2+4ax上,得出3k=a﹣4a,化简得到k=﹣a.再由△FCD与直角△AED相似,则△FCD是直角三角形,又∠FDC=∠ADE<90°,∠CFD<90°,得出∠FCD=90°,△FCD∽△AED.再根据两点之间的距离公式得出FC2=CD2=1+a2 , 得出△FCD是等腰直角三角形,则△AED也是等腰直角三角形,所以∠DAE=45°,由三角形内角和定理求出∠OBA=45°,那么OB=OA=4,即4k=4,求出k=1,a=﹣1,进而得到此二次函数的关系式为y=﹣x2﹣4x.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数y=x2+bx的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为2 ![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1 , 求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1 , 求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高. 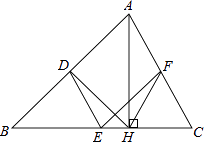
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D依次为一直线上4个点,BC=2,△BCE为等边三角形,⊙O过A、D、E3点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解2013年八年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%. 
类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
册数(本) | 128 | 80 | m | 48 |
(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角α的度数;
(2)该校2013年八年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校“振兴阅读工程”的开展情况,教育部门对该校初中生的阅读情况进行了随机问卷调查,绘制了如下图表: 初中生喜爱的文学作品种类调查统计表
种类 | 小说 | 散文 | 传记 | 科普 | 军事 | 诗歌 | 其他 |
人数 | 72 | 8 | 21 | 19 | 15 | 2 | 13 |

根据上述图表提供的信息,解答下列问题:
(1)喜爱小说的人数占被调查人数的百分比是多少?初中生每天阅读时间的中位数在哪个时间段内?
(2)将写读后感、笔记积累、画圈点读等三种方式称为有记忆阅读.请估计该校现有的2000名初中生中,能进行有记忆阅读的人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ![]() ,反比例函数y=
,反比例函数y= ![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com