
【题目】
(1)![]() ﹣|﹣2|+(﹣2)0;
﹣|﹣2|+(﹣2)0;
(2)(x+1)(x﹣1)﹣(x﹣2)2 .
【答案】
(1)解:原式=3﹣2+1=2;
(2)解:原式=x2﹣1﹣x2+4x﹣4=4x﹣5.
【解析】(1)原式第一项利用平方根定义化简,第二项利用绝对值的代数意义化简,最后一项利用零指数幂法则计算即可得到结果;(2)原式第一项利用平方差公式化简,第二项利用完全平方公式展开,去括号合并即可得到结果.
【考点精析】本题主要考查了零指数幂法则和实数的运算的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);先算乘方、开方,再算乘除,最后算加减,如果有括号,先算括号里面的,若没有括号,在同一级运算中,要从左到右进行运算才能正确解答此题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有1个红球、1个黄球和1个白球,这些球除颜色外都相同
(1)搅匀后从袋子中任意摸出1个球,求摸到红球的概率;
(2)搅匀后从袋子中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球,求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=36°,

(1)作出AB边的垂直平分线DE,交AC于点D,交AB于点E,连接BD;
(2)下列结论正确的是:
① BD平分∠ABC;② AD=BD=BC;③ △BDC的周长等于AB+BC; ④ D点是AC中点;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC﹣CD﹣DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2). 
(1)当t=2时,求S的值;
(2)当点P在边DA上运动时,求S关于t的函数表达式;
(3)当S=12时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.
(1)求点A的坐标;
(2)设二次函数图象的顶点为F,其对称轴与直线AB及x轴分别交于点D和点E,若△FCD与△AED相似,求此二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,一次函数y=﹣ ![]() x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方. 
(1)若直线AB与 ![]() 有两个交点F、G. ①求∠CFE的度数;
有两个交点F、G. ①求∠CFE的度数;
②用含b的代数式表示FG2 , 并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=a(x2﹣2mx﹣3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.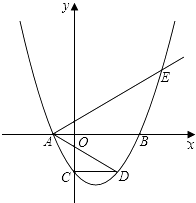
(1)用含m的代数式表示a;
(2)求证: ![]() 为定值;
为定值;
(3)设该二次函数图象的顶点为F,探索:在x轴的负半轴上是否存在点G,连接GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( ) 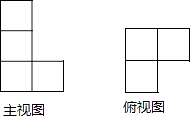
A.10
B.11
C.12
D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com