
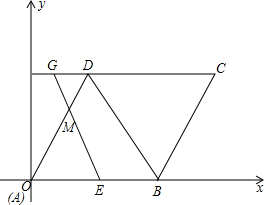
 如图,菱形ABCD的顶点A与平面直角坐标系中的点O重合,AB在X轴上,其边长为6cm,∠DAB=60°,点M是AD一点,且DM=2cm,点E、F分别从A、D两点同时出发,E点以每秒1cm的速度沿A→B向B点运动,F点以每秒⒉5cm的速度沿D→C→B→A运动.当一点到达终点时,另一点立即停止运动.EM、CD的延长线相交于点G.
如图,菱形ABCD的顶点A与平面直角坐标系中的点O重合,AB在X轴上,其边长为6cm,∠DAB=60°,点M是AD一点,且DM=2cm,点E、F分别从A、D两点同时出发,E点以每秒1cm的速度沿A→B向B点运动,F点以每秒⒉5cm的速度沿D→C→B→A运动.当一点到达终点时,另一点立即停止运动.EM、CD的延长线相交于点G.分析 (1)根据菱形的四条边都相等,菱形ABCD的顶点A与平面直角坐标系中的点O重合,AB在X轴上,其边长为6cm,∠DAB=60°,可以求得点D的坐标,从而可以求得点C的坐标;
(2)根据题意,可知存在EF⊥BD,此时BE=BF即可,然后根据条件进行计算即可求得此时的时间t的值;
(3)先求出抛物线的解析式,从而可以求得抛物线的对称轴,而题目中点F运动的快,点E运动的慢,所以不存在某一时刻t,使直线EF恰为过O、D、C三点的抛物线的对称轴,只有改变点F的速度才可以使得直线EF恰为过O、D、C三点的抛物线的对称轴,从而求出点F改变后的速度;
(4)根据题目中的信息,我们可以得到点F的四种情况,然后进行分类讨论,得出点F在不同情况下,△EFG的面积为S与t的函数关系式.
解答 解:(1)如下图所示:作DH⊥AB于点H.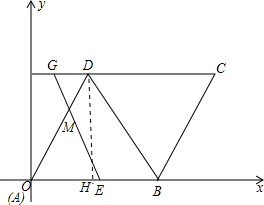
∵∠DAH=60°,AD=6,
∴OH=AD×cos60°=6×$\frac{1}{2}$=3,DH=AD×sin60°=6×$\frac{\sqrt{3}}{2}$=$3\sqrt{3}$.
∴点D的坐标为(3,$3\sqrt{3}$).
∵菱形ABCD的顶点A与平面直角坐标系中的点O重合,AB在X轴上,其边长为6cm,
∴点C的横坐标为:OH+CD=3+6=9,纵坐标为:$3\sqrt{3}$.
∴点C的坐标为(9,3$\sqrt{3}$).
即点C的坐标为(9,3$\sqrt{3}$),点D的坐标为(3,$3\sqrt{3}$).
(2)存在某一时刻t,使EF⊥BD,如下图所示: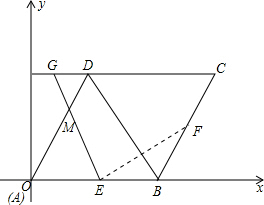
∵点E、F分别从A、D两点同时出发,E点以每秒1cm的速度沿A→B向B点运动,F点以每秒⒉5cm的速度沿D→C→B→A运动,若EF⊥BD,
∴BE=6-t,BF=12-2.5t,BE=BF.
∴6-t=12-2.5t.
解得,t=4.
即t=4s时,EF⊥BD.
(3)不存在某一时刻t,使直线EF恰为过O、D、C三点的抛物线的对称轴.
理由:设过O、D、C三点的抛物线的解析式为:y=ax2+bx+c.
∵点O的坐标为(0,0),点C的坐标为(9,3$\sqrt{3}$),点D的坐标为(3,$3\sqrt{3}$).
∴$\left\{\begin{array}{l}{c=0}\\{81a+9b+c=3\sqrt{3}}\\{9a+3b+c=3\sqrt{3}}\end{array}\right.$.
解得,a=$-\frac{\sqrt{3}}{9}$,b=$\frac{4\sqrt{3}}{3}$,c=0.
∴$y=-\frac{\sqrt{3}}{9}{x}^{2}+\frac{4\sqrt{3}}{3}x$,对称轴为直线x=$-\frac{b}{2a}=-\frac{\frac{4\sqrt{3}}{3}}{2×(-\frac{\sqrt{3}}{9})}=6$.
∵点E点以每秒1cm的速度沿A→B向B点运动,F点以每秒⒉5cm的速度沿D→C→B→A运动,
∴点E运动的慢,点F运动的快,不可能使得直线EF恰为过O、D、C三点的抛物线的对称轴.
若使直线EF恰为过O、D、C三点的抛物线的对称轴,则需要改变点F的速度,
设点F的速度为每秒运动xcm,
则$\frac{6}{1}=\frac{6-3}{x}$.
解得,x=0.5.
即点F的速度为0.5cm/s时,可以使直线EF恰为过O、D、C三点的抛物线的对称轴.
(4)根据题目中的信息可知,存在四种情况,
第一种情况:当点F在CD段时,如下图所示: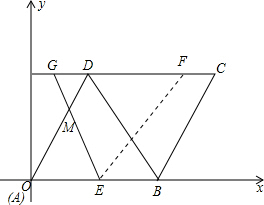
由题意可得,△DMC∽△AME,
∴$\frac{DM}{AM}=\frac{GD}{OE}$.
∵DM=2,AM=4,
∴$\frac{GD}{OE}=\frac{1}{2}$.
点F由点D到点C的最大时间为:6÷2.5=2.4s.
∴${S}_{△EFG}=\frac{(\frac{1}{2}t+2.5t)×3\sqrt{3}}{2}=4.5\sqrt{3}{t}^{2}$(0<t≤2.4).
第二种情况:当点F在CB段时,如下图所示: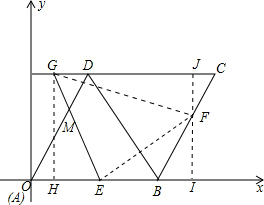
作GH⊥x轴于点H,JI⊥x轴于点I
由题意可得,△DMC∽△AME,
∴$\frac{DM}{AM}=\frac{GD}{OE}$.
∵DM=2,AM=4,
∴$\frac{GD}{OE}=\frac{1}{2}$.
点F由点D到点C的最大时间为:6÷2.5=2.4s.
点F由点C到点B的最大时间为:6÷2.5=2.4s.
故点F由C到B用的时间取值范围为为:2.4<t<4.8.
由题意可得,OH=3-$\frac{t}{2}$,CJ=(2.5t-6)cos60°=1.25t-3,FJ=(2.5t-6)sin60°=1.25$\sqrt{3}$t-3$\sqrt{3}$,GH=3$\sqrt{3}$,GD=$\frac{1}{2}t$,
∴HE=t-OH=$\frac{3t}{2}-3$,HI=9-OH-CJ=9-0.75t,EI=OI-OE=(9-CJ)-t=12-2.25t,FI=$3\sqrt{3}-FJ$=6$\sqrt{3}$-1.25$\sqrt{3}t$,GC=6+$\frac{1}{2}t$.
∴S△EFG
=S矩形GHIJ-S△GHE-S△EIF-S△FGC
=HI×HG-$\frac{HE×GH}{2}$$-\frac{EI×FI}{2}-\frac{CG×JF}{2}$
=(9-0.75t)×$3\sqrt{3}$-$\frac{(\frac{3}{2}t-3)×3\sqrt{3}}{2}$$-\frac{(12-2.25t)(6\sqrt{3}-1.25\sqrt{3}t)}{2}$$-\frac{(6+\frac{1}{2}t)(1.25\sqrt{3}t-3\sqrt{3})}{2}$
=$-\frac{45+10\sqrt{3}}{32}{t}^{2}+\frac{15\sqrt{3}t}{4}+\frac{9\sqrt{3}}{2}$(2.4<t<4.8).
第三种情况:当点F在AB段且在点E的右侧时,如下图所示: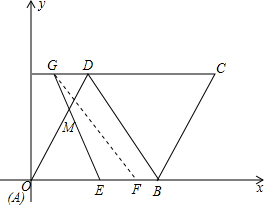
由题意可得,OE=t,BF=2.5t-12.
∴EF=6-OE-BF=18-3.5t.
当18-3.5t=0时,得t=$5\frac{1}{7}$.
∴${S}_{△GEF}=\frac{EF×3\sqrt{3}}{2}=\frac{54\sqrt{3}-10.5\sqrt{3}t}{2}$(4.8≤t<$5\frac{1}{7}$).
第四种情况:当点F在AB段且在点E的左侧时,如下图所示: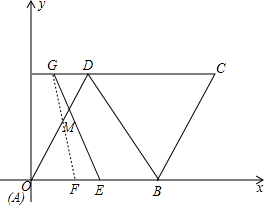
∵6÷1=6,18÷2.5=7.2,
∴点E先到到点B.
由题意可得,EF=OE+BF-6=t+2.5t-12-6=3.5t-18.
∴${S}_{△GEF}=\frac{(3.5t-18)×3\sqrt{3}}{2}=\frac{10.5\sqrt{3}t-54\sqrt{3}}{2}$($5\frac{1}{7}<t≤6$).
点评 本题考查根据菱形的性质和平面直角坐标系,求点的坐标的问题;猜想型问题,根据题目题目信息,可以得到动点在不同情况下,对应的函数关系式,还考查到三角形相似的知识,分类讨论数学思想贯穿于本题.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
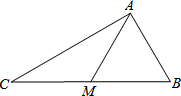 如图,△ABC中,∠B=60°,∠C=30°,AM是BC边上的中线,且AM=4,则△ABC的周长是( )
如图,△ABC中,∠B=60°,∠C=30°,AM是BC边上的中线,且AM=4,则△ABC的周长是( )| A. | 12 | B. | $12+4\sqrt{3}$ | C. | $12+2\sqrt{3}$ | D. | $6\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com