
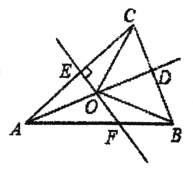
【题目】如图,在△ABC中,AB=AC,点D是C的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.
(1)求证:点O在AB的垂直平分线上;
(2)若∠CAD=20°,求∠BOF的度数.
【答案】(1)证明见解析;(2)30°.
【解析】
(1)根据等腰三角形的性质可得AD⊥BC,根据垂直平分线的性质可得BO=AO,依此即可证明点O在AB的垂直平分线上;
(2)根据等腰三角形的性质可得∠BAD=∠CAD=20°,∠CAB=40°,再根据垂直的定义,等腰三角形的性质和角的和差故选即可得到∠BOF的度数.
(1)证明:∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∵AD是BC的垂直平分线,
∴BO=CO,
∵OE是AC的垂直平分线,
∴AO=CO,
∴BO=AO,
∴点O在AB的垂直平分线上;
(2)解:∵AB=AC,点D是BC的中点,
∴AD平分∠BAC,
∵∠CAD=20°,
∴∠BAD=∠CAD=20°,∠CAB=40°,
∵OE⊥AC,
∴∠EFA=90°-40°=50°,
∵AO=CO,
∴∠OBA=∠BAD=20°,
∴∠BOF=∠EFA-∠OBA=50°-20°=30°.


科目:初中数学 来源: 题型:
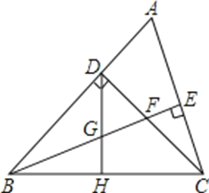
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, BM切⊙O于点B,点P是⊙O上的一个动点(不经过A,B两点),过O作OQ∥AP交![]() 于点Q,过点P作
于点Q,过点P作![]() 于C,交
于C,交![]() 的延长线于点E,连结
的延长线于点E,连结![]() .
.
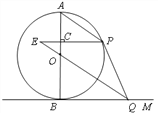
(1)求证:PQ与⊙O相切;
(2)若直径AB的长为12,PC=2EC,求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
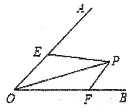
【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( )
A. 30°B. 45°C. 60°D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:

请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
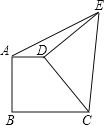
A. 1 B. 2 C. 3 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com