Question

下表中，y是x的一次函数．

x	2	1	2		5
y	6	3		12	15

 

（1）求该函数的表达式，并补全表格；

（2）已知该函数图象上一点M（1，-3）也在反比例函数图象上，求这两个函数图象的另一交点N的坐标．

 

Answer 1

（1）y=-3x，补全表格见解析；（2）（-1，3）．

【解析】

试题分析：（1）设y=kx+b，将任已知两点代入可得函数解析式，从而补全表格.

（2）将点M的坐标代入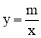，可得m的值，联立一次函数及反比例函数解析式可得另一交点坐标．

试题解析：【解析】
（1）设该一次函数为y=kx+b（k≠0），

∵当x=-2时，y=6，当x=1时，y=-3，

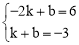∴，解得：.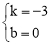

∴一次函数的表达式为：y=-3x.

∵当x=2时，y=-6；当y=-12时，x=4，

补全表格如下：

x	2	1	2	4	5
y	6	3	-6	12	15

（2）∵点M（1，-3）在反比例函数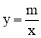上（m≠0），

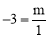∴，解得m=-3到.

∴反比例函数解析式为.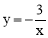

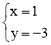联立可得，解得：或.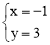

∴另一交点坐标为（-1，3）．

考点：1.反比例函数与一次函数的交点问题；2.待定系数法的应用；3.曲线上点的坐标与言重听取的关系.