Question

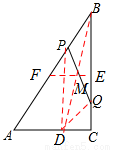
如图，Rt△ABC中，∠ACB＝90°，AC＝6 cm，BC＝8 cm，动点P从点B出发，在BA边上以每秒5 cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4 cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ.

（1）若△BPQ与△ABC相似，求t的值；

（2）连接AQ、CP，若AQ⊥CP，求t的值；

（3）试证明：PQ的中点在△ABC的一条中位线上.

 

 

Answer 1

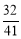（1）t=1或；（2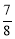）；（3）证明见解析.

【解析】

试题分析：（1）分两种情况讨论：①当△BPQ∽△BAC时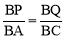， ，当△BPQ∽△BCA时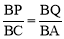， ，再根据BP=5t，QC=4t，AB=10cm，BC=8cm，代入计算即可.

（2）过P作PM⊥BC于点M，AQ，CP交于点N，则有PB=5t，PM=3t，MC=8-4t，根据△ACQ∽△CMP，得出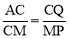 ，代入计算即可.

（3）过P作PD⊥AC于点D，连接DQ，BD，BD交PQ于点M，过点M作EF∥AC分别交BC，BA于E，F两点，

证明四边形PDQB是平行四边形，则点M是PQ和BD的中点，进而由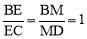得到点E为BC的中点，由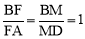得到点F为BA的中点，因此，PQ中点在△ABC的中位线上.

试题解析：（1）①当△BPQ∽△BAC时，

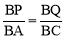∵ ，BP=5t，QC=4t，AB=10cm，BC=8cm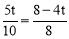，∴，解得t=1；

②当△BPQ∽△BCA时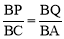，∵，∴ ，解得.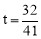

∴t=1或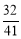时，△BPQ与△ABC相似.

（2）如答图，过P作PM⊥BC于点M，AQ，CP交于点N，则有PB=5t，PM=3t，MC=8-4t，

∵∠NAC+∠NCA=90°，∠PCM+∠NCA=90°，∴∠NAC=∠PCM且∠ACQ=∠PMC=90°，

∴△ACQ∽△CMP.∴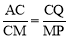.∴ 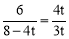，解得：.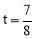

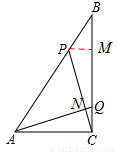
（3）如答图，过P作PD⊥AC于点D，连接DQ，BD，BD交PQ于点M，

则，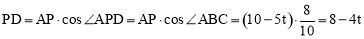

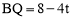∵，∴PD=BQ且PD∥BQ.∴四边形PDQB是平行四边形.∴点M是PQ和BD的中点.

过点M作EF∥AC分别交BC，BA于E，F两点，

则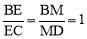，即点E为BC的中点.

同理，点F为BA的中点.

∴PQ中点在△ABC的中位线上.

考点：1.双动点问题；2.相似三角形的判定和性质；3平行四边形的判定和性质；4.三角形中位线的判定.．