
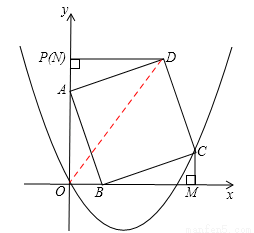
如图,在平面直角坐标系中,已知点P(0,4),点A在线段OP上,点B在x轴正半轴上,且AP=OB=t, 0<t<4,以AB为边在第一象限内作正方形ABCD;过点C、D依次向x轴、y轴作垂线,垂足为M,N,设过O,C两点的抛物线为y=ax2+bx+c.
(1)填空:△AOB≌△ ≌△BMC(不需证明);用含t的代数式表示A点纵坐标:A(0, ;
(2)求点C的坐标,并用含a,t的代数式表示b;
(3)当t=1时,连接OD,若此时抛物线与线段OD只有唯一的公共点O,求a的取值范围;
(4)当抛物线开口向上,对称轴是直线 ,顶点随着t的增大向上移动时,求t的取值范围.
,顶点随着t的增大向上移动时,求t的取值范围.

(1)DNA或△DPA;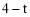 ;(2)C(4,t),
;(2)C(4,t),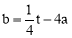 ;(3)a>0或a<
;(3)a>0或a<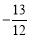 或
或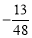 <a<0;(4)
<a<0;(4)
0<t≤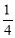 .
.
【解析】
试题分析:(1)根据全等三角形的判定定理SAS证得:△AOB≌△DNA或DPA≌△BMC;根据图中相关线段间的和差关系来求点A的坐标:
∵∠DNA=∠AOB=90°,∴∠NAD=∠OBA(同角的余角相等).
在△AOB与△DNA中,∵ ,∴△AOB≌△DNA(SAS).
,∴△AOB≌△DNA(SAS).
同理△DNA≌△BMC.
∵点P(0,4),AP=t,∴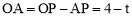 .
.
(2)利用(1)中的全等三角形的对应边相等易推知:OM=OB+BM=t+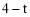 =4,则C(4,t).把点O、C的坐标分别代入抛物线y=ax2+bx+c可以求得
=4,则C(4,t).把点O、C的坐标分别代入抛物线y=ax2+bx+c可以求得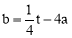 确.
确.
(3)利用待定系数法求得直线OD的解析式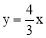 .与抛物线联立方程组,解得x=0或
.与抛物线联立方程组,解得x=0或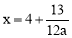 .
.
对于抛物线的开口方向进行分类讨论,即a>0和a<0两种情况下的a的取值范围.
(4)根据抛物线的解析式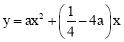 得到顶点坐标是
得到顶点坐标是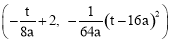 .结合已知条件求得a=
.结合已知条件求得a=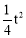 ,故顶点坐标为
,故顶点坐标为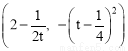 .由抛物线的性质知:只与顶点坐标有关,故t的取值范围为:0<t≤
.由抛物线的性质知:只与顶点坐标有关,故t的取值范围为:0<t≤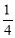 .
.
试题解析:【解析】
(1)DNA或△DPA;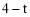 .
.
(2)由题意知,NA=OB=t,则OA= 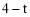 .
.
∵△AOB≌△BMC,∴CM=OB=t. ∴OM=OB+BM=t+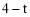 =4. ∴C(4,t).
=4. ∴C(4,t).
又抛物线y=ax2+bx+c过点O、C,
∴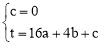 ,解得
,解得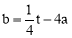 .
.
(3)当t=1时,抛物线为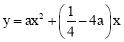 ,NA=OB=1,OA=3.
,NA=OB=1,OA=3.
∵△AOB≌△DNA,∴DN=OA=3.
∵D(3,4),∴直线OD为: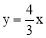 .
.
联立方程组,得 ,消去y,得
,消去y,得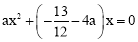 ,
,
解得,x=0或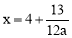 .
.
所以,抛物线与直线OD总有两个交点.
讨论:①当a>0时,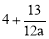 >3,只有交点O,所以a>0符合题意;
>3,只有交点O,所以a>0符合题意;
②当a<0时,若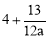 >3,则a<
>3,则a<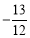 ;
;
若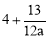 <0,则得a>
<0,则得a>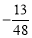 .∴
.∴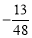 <a<0.
<a<0.
综上所述,a的取值范围是a>0或a<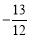 或
或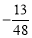 <a<0.
<a<0.
(4)∵抛物线为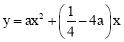 ,∴顶点坐标是
,∴顶点坐标是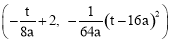 .
.
又∵对称轴是直线x=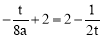 ,∴a=
,∴a=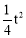 .
.
∴顶点坐标为: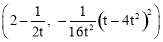 ,即
,即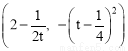 .
.
∵抛物线开口向上,且随着t的增大,抛物线的顶点向上移动,
∴只与顶点坐标有关,∴t的取值范围为:0<t≤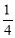 .
.
考点:1.二次函数综合题;2.线动平移问题;3.全等三角形的判定和性质;4.待定系数法的应用;5.曲线上点的坐标与方程的关系;6.二次函数的性质;7.平移的性质;8.分类思想的应用.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:解答题
下表中,y是x的一次函数.
x |
| 1 | 2 |
| 5 |
y | 6 |
|
|
|
|
(1)求该函数的表达式,并补全表格;
(2)已知该函数图象上一点M(1,-3)也在反比例函数 图象上,求这两个函数图象的另一交点N的坐标.
图象上,求这两个函数图象的另一交点N的坐标.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=( )

A. ∠ACD B. ∠ADB C. ∠AED D. ∠ACB
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:解答题
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
根据以上信息解答下列问题:


(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:选择题
计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com