
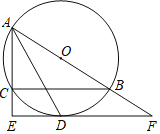
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=8,CE=4,求弧BD的长.(结果保留π)
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由OA=OD知∠OAD=∠ODA,由AD平分∠EAF知∠DAE=∠DAO,据此可得∠DAE=∠ADO,继而知OD∥AE,根据AE⊥EF即可得证;
(2)作OG⊥AE,知AG=CG=![]() AC=4,证四边形ODEG是矩形,得出OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=192,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
AC=4,证四边形ODEG是矩形,得出OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=192,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
(1)证明:连接OD,如图1所示:

∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠EAF,
∴∠DAE=∠DAO,
∴∠DAE=∠ADO,
∴OD∥AE,
∵AE⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:作OG⊥AE于点G,连接BD,如图2所示:
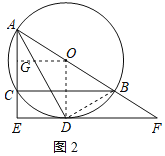
则AG=CG=![]() AC=4,∠OGE=∠E=∠ODE=90°,
AC=4,∠OGE=∠E=∠ODE=90°,
∴四边形ODEG是矩形,
∴OA=OB=OD=CG+CE=4+4=8,∠DOG=90°,
∴AB=2OA=16,
∵AC=8,CE=4,
∴AE=AC+CE=12,
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在Rt△ABD中,![]() ,
,
在Rt△ABD中,∵AB=2BD,
∴∠BAD=30°,
∴∠BOD=60°,
则弧BD的长度为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
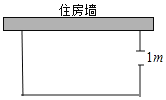
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
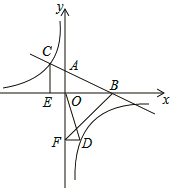
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
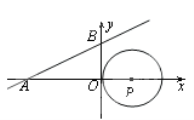
【题目】如图,直线y=![]() x+
x+![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千 克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)(3分)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)(3分)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)(4分)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于![]() AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
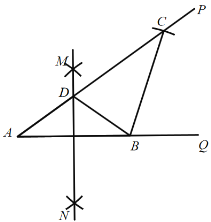
A.∠CDB=72°B.△ADB∽△ABCC.CD:AD=2:1D.∠ABC=3∠ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.
的图象与性质时,我们对函数解析式进行了深入分析.
首先,确定自变量![]() 的取值范围是全体非零实数,因此函数图象会被
的取值范围是全体非零实数,因此函数图象会被![]() 轴分成两部分;其次,分析解析式,得到
轴分成两部分;其次,分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于零,随着
的值减小,且逐渐接近于零,随着![]() 值的减小,
值的减小,![]() 的值会越来越大…,由此,可以大致画出
的值会越来越大…,由此,可以大致画出![]() 在
在![]() 时的部分图象,如图所示:
时的部分图象,如图所示:
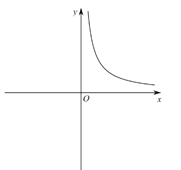
利用同样的方法,我们可以研究函数![]() 的图象与性质.通过分析解析式画出部分函数图象如图所示.
的图象与性质.通过分析解析式画出部分函数图象如图所示.
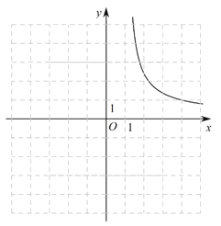
(1)请沿此思路在图中完善函数图象的草图并标出此函数图象上横坐标为0的点![]() ;(画出网格区域内的部分即可)
;(画出网格区域内的部分即可)
(2)观察图象,写出该函数的一条性质:__________;
(3)若关于![]() 的方程
的方程![]() 有两个不相等的实数根,结合图象,直接写出实数
有两个不相等的实数根,结合图象,直接写出实数![]() 的取值范围: __________.
的取值范围: __________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有专家指出:人为型空气污染(如汽车尾气排放等)是雾霾天气的重要成因.某校为倡议“每人少开一天车,共建绿色家园”,想了解学生上学的交通方式.九年级(8)班的5名同学联合设计了一份调查问卷.对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,扇形统计图中“骑自行车”所在扇形的圆心角度数是 度,请补全条形统计图;
(2)已知这5名学生中有2名女同学,要从这5名学生中任选两名同学汇报调查结果.请用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①abc>0;
②b2﹣4ac>0;
③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;
⑤5a﹣2b+c<0.
其中正确的个数有( )
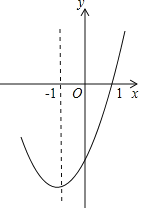
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com