
【题目】如图△ABC中,延长BC到D,∠ABC和∠ACD的平分线相交于P.
(1)若∠A=60°,则∠P= .
(2)请你用数学表达式归纳出∠P与∠A的关系: .
(3)请说明你的结论(2)正确的理由.

【答案】(1)30°;(2)∠P=![]() ∠A;(3)理由见解析.
∠A;(3)理由见解析.
【解析】
(1)PB、PC分别平分∠ABC和∠ACD,得出∠ACD=2∠PCD,∠ABC=2∠PBC,而∠PCD=∠P+∠PBC,∠ACD=∠ABC+∠A,∠A=2∠P,∠P=![]() ∠A,由此即可得出结论;
∠A,由此即可得出结论;
(2)(3)根据规律,∠P的度数等于∠A的一半;根据三角形的一个外角等于和它不相邻的两个内角的和表示出∠P,再根据角平分线的定义∠PCD=![]() ∠ACD,∠PBC=
∠ACD,∠PBC=![]() ∠ABC,代入求解即可.
∠ABC,代入求解即可.
解:(1)∵PB、PC分别平分∠ABC和∠ACD,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∵∠PCD=∠P+∠PBC,∠ACD=∠ABC+∠A,
∴∠A=2∠P,即∠P=![]() ∠A,
∠A,
∵∠A=60°,
∴∠P=30°.
故答案为:30°;
(2)∠P=![]() ∠A,
∠A,
故答案为:∠P=![]() ∠A;
∠A;
(3)理由:∵PB,PC是∠ABC和∠ACD的平分线,
∴∠PCD=![]() ∠ACD,∠PBC=
∠ACD,∠PBC=![]() ∠ABC,
∠ABC,
∴∠P=∠PCD﹣∠PBC,
=![]() ∠ACD﹣
∠ACD﹣![]() ∠ABC,
∠ABC,
=![]() (∠ACD﹣∠ABC),
(∠ACD﹣∠ABC),
=![]() ∠A,
∠A,
即∠P=![]() ∠A.
∠A.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
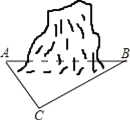
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:


根据以上信息,整理分析数据如下:

(1)写出表格中a,b,c的值;
(2)分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:综合实践活动课上,同学们围绕“已知三角形三边的长度,求三角形的面积”开展活动,启航小组同学想到借助正方形网格解决问题
问题解决:图(1)、图(2)都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,操作发现,启航小组同学在图(1)中画出△ABC,其顶点A,B,C都在格点上,同时构造长方形CDEF,使它的顶点都在格点上,且它的边EF经过点A,ED经过点B.同学们借助此图求出了△ABC的面积.
(1)在图(1)中,△ABC的三边长分别是AB= ,BC= ,AC= .△ABC的面积是 .
(2)已知△PMN中,PM=![]() ,MN=2
,MN=2![]() ,NP=
,NP=![]() .请你根据启航小组的思路,在图(2)中画出△PMN,并直接写出△RMN的面积 .
.请你根据启航小组的思路,在图(2)中画出△PMN,并直接写出△RMN的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(1,1),B(3,3),动点C在x轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 、
、![]() 分别为线段
分别为线段![]() 上的两个动点,且
上的两个动点,且![]() 于
于![]() ,
,![]() 于
于![]() ,若
,若![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() ,
,![]() ;
;
(2)当![]() ,
,![]() 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com