
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

【答案】(1)10;30;(2)y=![]() ;(3)登山3分钟、10分钟或13分钟
;(3)登山3分钟、10分钟或13分钟
【解析】
(1)根据速度=高度÷时间即可算出甲登山上升的速度; 根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;
(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;
(3)当乙未到终点时, 找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程, 解之即可求出x值;当乙到达终点时,用终点的高度-甲登山全程中y关于x的函数关系式=50,即可得出关于x的一元一次方程, 解之可求出x值.综上即可得出结论.
(1)甲登山上升的速度是:(300﹣100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30;
(2)当0≤x<2时,y=15x;
当x≥2时,y=30+10×3(x﹣2)=30x﹣30.
当y=30x﹣30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=![]() ;
;
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100﹣(30x﹣30)=70时,解得:x=3;
当30x﹣30﹣(10x+100)=70时,解得:x=10;
当300﹣(10x+100)=70时,解得:x=13.
答:登山3分钟、10分钟或13分钟时,甲、乙两人距地面的高度差为70米.


科目:初中数学 来源: 题型:
【题目】如图,过圆外一点P作⊙O的两条切线,切点分别为A、B,连接AB,在AB、PB、PA上分别取一点D、E、F,使AD=BE,BD=AF,连接DE、DF、EF,则∠EDF等于( )
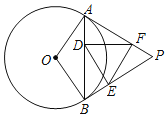
A.90°﹣∠PB.90°﹣![]() ∠PC.180°﹣∠PD.45°﹣
∠PC.180°﹣∠PD.45°﹣![]() ∠P
∠P
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.

(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,BA=5,点D是边AC上的一动点,过点D作DE∥AB交边BC于点E,过点B作BF⊥BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,AD的长度为______.
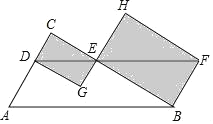
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
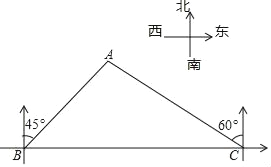
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,当自变量![]() 取
取![]() 时,函数值
时,函数值![]() 等于
等于![]() ,我们称
,我们称![]() 为这个函数的“二合点”.如果二次函数
为这个函数的“二合点”.如果二次函数![]() 有两个相异的二合点
有两个相异的二合点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com