
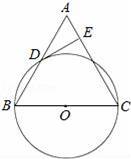
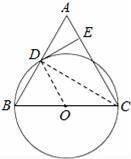
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=
 ,求DE的长.
,求DE的长.

【考点】切线的判定与性质;勾股定理;圆周角定理;解直角三角形.
【分析】(1)连接CD,由BC为直径可知CD⊥AB,又BC=AC,由等腰三角形的底边“三线合一”证明结论;
(2)连接OD,则OD为△ABC的中位线,OD∥AC,已知DE⊥AC,可证DE⊥OC,证明结论;
(3)连接CD,在Rt△BCD中,已知BC=18,cosB=
 ,求得BD=6,则AD=BD=6,在Rt△ADE中,已知AD=6,cosA=cosB=
,求得BD=6,则AD=BD=6,在Rt△ADE中,已知AD=6,cosA=cosB=
 ,可求AE,利用勾股定理求DE.
,可求AE,利用勾股定理求DE.
【解答】(1)证明:连接CD,
∵BC为⊙O的直径,∴CD⊥AB,
又∵AC=BC,
∴AD=BD,即点D是AB的中点.
(2)解:DE是⊙O的切线.
证明:连接OD,则DO是△ABC的中位线,
∴DO∥AC,
又∵DE⊥AC,
∴DE⊥DO即DE是⊙O的切线;
(3)解:∵AC=BC,∴∠B=∠A,
∴cosB=cosA=
 ,
,
∵cosB=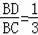
 ,BC=18,
,BC=18,
∴BD=6,
∴AD=6,
∵cosA=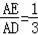
 ,
,
∴AE=2,
在Rt△AED中,DE=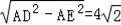
 .
.

【点评】本题考查了切线的判定与性质,勾股定理,圆周角定理,解直角三角形的运用,关键是作辅助线,将问题转化为直角三角形,等腰三角形解题.


科目:初中数学 来源: 题型:
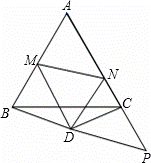
如图,已知△ABC中,AB=AC=1,∠ABC=∠ACB=60°,点D是△ABC外一点,且BD=DC,∠DBC=∠DCB=30°,又点M、N分别在AB、AC上,∠MDN=60°,小明为探求△AMN的周长,在AC的延长线上截取了CP=BM,并连接DP,
(1)试说明:MN=NP;
(2)求出△AMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
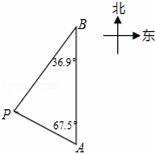
日本福岛出现核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场监测与海水采样,针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估.如图,上午9时,海检船位于A处,观测到某港口城市P位于海检船的北偏西67.5°方向,海检船以21海里/时 的速度向正北方向行驶,下午2时海检船到达B处,这时观察到城市P位于海检船的南偏西36.9°方向,求此时海检船所在B处与城市P的距离?
(参考数据: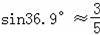
 ,
,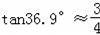
 ,
,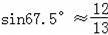
 ,
,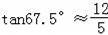
 )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com