
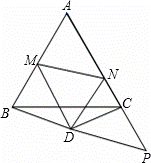
如图,已知△ABC中,AB=AC=1,∠ABC=∠ACB=60°,点D是△ABC外一点,且BD=DC,∠DBC=∠DCB=30°,又点M、N分别在AB、AC上,∠MDN=60°,小明为探求△AMN的周长,在AC的延长线上截取了CP=BM,并连接DP,
(1)试说明:MN=NP;
(2)求出△AMN的周长.
略;2.
详解:(1)∵∠ABC=∠ACB=60°,∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
在△MBD和△PCD中,MB=PC,∠ABD=∠ACD,BD=CD,
∴△MBD≌△PCD(SAS),
∴MD=PD,∠MDB=∠PDC,
又∵∠DBC=∠DCB=30°,∴∠BDC=120°,
∴∠MDB+∠MDC=120°,
∴∠PDC+∠MDC=120°,即∠PDM=120°,
又∵∠MDN=60°,∴∠PDN=60°,
∴∠MDN=∠PDN=60°,
在△MDN和△PDN中,MD=PD,∠MDN=∠PDN,DN=DN,
∴△MDN≌△PDN(SAS),∴MN=NP;
(2)△AMN的周长:
AM+MN+AN=AM+NP+AN=AM+AP=AM+AC+CP=AM+AC+BM=AB+AC=1+1=2;
∴△AMN的周长为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.
若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A. 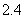 B. 4 C.
B. 4 C. 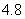 D. 5
D. 5

查看答案和解析>>
科目:初中数学 来源: 题型:
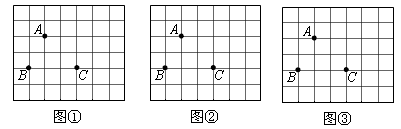
下图均为7×6的正方形网格,点A、B、C在格点上.在图中确定格点D,并画出以点A、B、C、D为顶点的四边 形,使其为轴对称图形.(要求:分别在图①、图②、图③中画出三个互不相同的图形)
形,使其为轴对称图形.(要求:分别在图①、图②、图③中画出三个互不相同的图形)
查看答案和解析>>
科目:初中数学 来源: 题型:
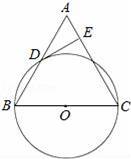
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=
 ,求DE的长.
,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com