
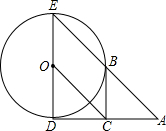
 如图,已知⊙O的半径为1,DE是⊙O的直径,过D点作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,若四边形BCOE是平行四边形,
如图,已知⊙O的半径为1,DE是⊙O的直径,过D点作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,若四边形BCOE是平行四边形,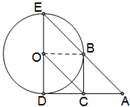 证明:(1)连接OB
证明:(1)连接OB

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
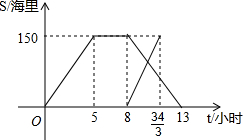 一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com