
分析 (1)设可租用甲种货车x辆,乙种货车(8-x)辆,因为要一次性运送,所以所装的货物应该不少于60个床架和100套桌椅,根据题目所给的其他条件可列出不等式组.
(2)因为甲种货车每辆须付运费1200元,乙种货车要付1000元,所以乙种货车越多越省钱.选择方案可算出费用.
解答 解:(1)设可租用甲种货车x辆,乙种货车(8-x)辆,依题意有
$\left\{\begin{array}{l}{5x+10(8-x)≥60}\\{20x+10(8-x)≥100}\end{array}\right.$,
解得2≤x≤4.
故甲有3种方案:①甲2辆,乙6辆.
②甲3辆,乙5辆.
③甲4辆,乙4辆.
(2)①种方案最省钱.
1200×2+1000×6=8400(元).
选择①种方案,运费是8400元.
点评 本题考查了一元一次不等式组的应用以及理解题意能力,关键是货车能把床架和桌椅运走列出不等式组,找出方案,然后根据乙车越多越省钱,求出运费.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有四张背面相同的纸牌.请你用这四张牌计算“24点”,请列出四个符合要求的不同算式.【可运用加、减、乘、除、乘方(例如数2,6,可列62=36或26=64)运算,可用括号;注意:例如4×(1+2+3)=24与(2+1+3)×4=24只是顺序不同,属同一个算式】.
如图,有四张背面相同的纸牌.请你用这四张牌计算“24点”,请列出四个符合要求的不同算式.【可运用加、减、乘、除、乘方(例如数2,6,可列62=36或26=64)运算,可用括号;注意:例如4×(1+2+3)=24与(2+1+3)×4=24只是顺序不同,属同一个算式】.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
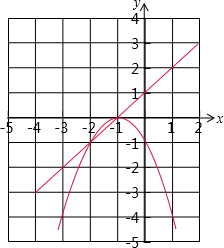 设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).
设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
如图,点A,B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com