
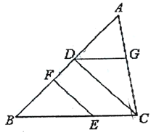
【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )

A. AD=CE B. MF=![]() CF C. ∠BEC=∠CDA D. AM=CM
CF C. ∠BEC=∠CDA D. AM=CM
【答案】D
【解析】
由等边三角形的性质和已知条件证出△AEC≌△BDA,即可得出A正确;
由全等三角形的性质得出∠BAD=∠ACE,求出∠CFM=∠AFE=60°,得出∠FCM=30°,即可得出B正确;由等边三角形的性质和三角形的外角性质得出C正确;D不正确.
A正确;理由如下:
∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC
又∵AE=BD
在△AEC与△BDA中,
 ,
,
∴△AEC≌△BDA(SAS),
∴AD=CE;
B正确;理由如下:
∵△AEC≌△BDA,
∴∠BAD=∠ACE,
∴∠AFE=∠ACE+∠CAD=∠BAD+∠CAD=∠BAC=60°,
∴∠CFM=∠AFE=60°,
∵CM⊥AD,
∴在Rt△CFM中,∠FCM=30°,
∴MF=![]() CF;
CF;
C正确;理由如下:
∵∠BEC=∠BAD+∠AFE,∠AFE=60°,
∴∠BEC=∠BAD+∠AFE=∠BAD+60°,
∵∠CDA=∠BAD+∠CBA=∠BAD+60°,
∴∠BEC=∠CDA;
D不正确;理由如下:
要使AM=CM,则必须使∠DAC=45°,由已知条件知∠DAC的度数为大于0°小于60°均可,
∴AM=CM不成立;
故选:D.


科目:初中数学 来源: 题型:
【题目】小明和小亮玩扑克牌游戏,小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌都为![]() 张,且
张,且![]() ;
;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出五张,放入中间一堆
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
(1)填写下表中的空格:
步骤 | 左边一堆牌的张数 | 中间一堆牌的张数 | 右边一堆牌的张数 |
第一步后 |
|
|
|
第二步后 |
|
| |
第三步后 |
|
| |
第四步后 |
|
(2)如若第四步完成后,中间一堆牌的张数的2倍恰好是右边一堆牌的张数的3倍,试求第一步后,每堆牌各有多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,![]() ,
,![]() ,垂足分别为D、F,
,垂足分别为D、F,![]() ,请试说明
,请试说明![]() .
.
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (____________________________)
(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
又∵![]() (已知)
(已知)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.
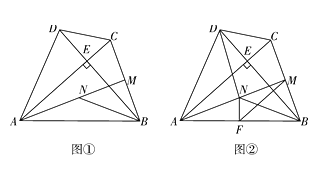
(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机王师傅某天早上营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天早上所接六位乘客的行车里程(![]() )如下:
)如下:
2,+5,-4,+1,-6,-2
(1)将最后一位乘客送到目的地时,王师傅在早上出发点的什么位置?
(2)若汽车耗油量为![]() ,这天早上王师傅接送乘客,出租车共耗油多少升?
,这天早上王师傅接送乘客,出租车共耗油多少升?
(3)若出租车起步价为6元,起步里程为![]() (包括
(包括![]() ),超过部分(不足
),超过部分(不足![]() 按
按![]() 计算)每千米1.5元,王师傅这天早上共得车费多少元?
计算)每千米1.5元,王师傅这天早上共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )
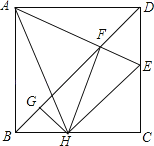
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
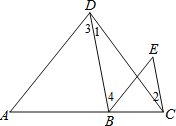
已知:如图,∠1=∠2,∠3=∠E.
求证:AD∥BE.
证明:∵∠1=∠2 (已知)
∴_____∥_____
(________)
∴∠E=∠_____
(________)
又∵∠E=∠3 ( 已知 )
∴∠3=∠_____
(________)
∴AD∥BE.
(________)
查看答案和解析>>
科目:初中数学 来源: 题型:
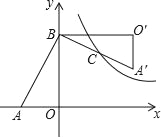
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
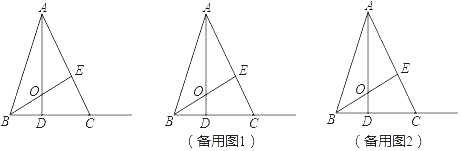
【题目】如图,在△ABC中,BC=5,高AD、BE相交于点O,BD=![]() CD,且AE=BE.
CD,且AE=BE.
(1)求线段AO的长;
(2)动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,△POQ的面积为S,请用含t的式子表示S,并直接写出相应的t的取值范围;
(3)在(2)的条件下,点F是直线AC上的一点且CF=BO.是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请直接写出符合条件的t值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com