
【题目】科技馆是少年儿童节假日游玩的乐园.如图所示,图中点的横坐标表示科技馆从8:30开门后经过的时间(分钟),纵坐标表示到达科技馆的总人数.图中曲线对应的函数解析式为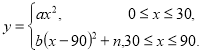 ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
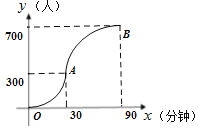
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
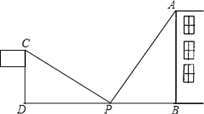
【题目】为了测量一幢高楼高AB,在旗杆CD与最右边的高楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=38°,测楼顶A视线PA与地面夹角∠APB=52°,量得P到楼底距离PB与旗杆CD高度相等,等于8米,量得旗杆与楼之间距离为DB=33米,求楼高AB是多少米?(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
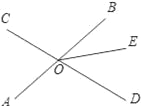
【题目】如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.
(1)求∠BOE和∠AOE的度数;
(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
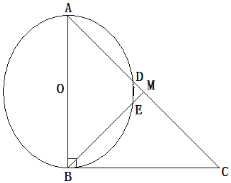
(1)求证:MD=ME
(2)填空:①若AB=6,当AD=2DM时,DE=___________;
②连接OD,OE,当∠A的度数为____________时,四边形ODME是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数y的最小值为5,则h的值是( )
A. ﹣1 B. ﹣1或5 C. 5 D. ﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解实际问题
华联商厦进货员在广州发现一种饰品,预计能畅销市场,就用8000元购进所有饰品,每件按58元很快卖完. 由于销路很好,又在上海用13200元购进,这次比在广州多进了100件,单价比广州贵了10%,但商厦仍按原售价销售,最后剩下的15件按八折销售,很快售完,问该商厦这两批饰品生意共赚了多少 ?(不考虑其它因素)
查看答案和解析>>
科目:初中数学 来源: 题型:
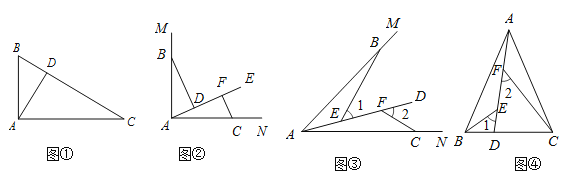
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=![]() ,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC. 求证:△ABE≌△CAF;
(3)拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com