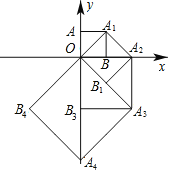
【题目】如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA1A2B1，…，依此规律，则点A8的坐标是（ ）
A．（﹣8，0） B．（0，8） C．（0，8
） D．（0，16）
【答案】D
【解析】
试题分析：根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以
，所以可求出从A到A3的后变化的坐标，再求出A1、A2、A3、A4、A5，得出A8即可．
解：根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以，
∵从A到A3经过了3次变化，
∵45°×3=135°，1×（）3=2．
∴点A3所在的正方形的边长为2，点A3位置在第四象限．
∴点A3的坐标是（2，﹣2）；
可得出：A1点坐标为（1，1），
A2点坐标为（0，2），
A3点坐标为（2，﹣2），
A4点坐标为（0，﹣4），A5点坐标为（﹣4，﹣4），
A6（﹣8，0），A7（﹣8，8），A8（0，16），
故选：D．
科目：初中数学 来源： 题型：
【题目】下列计算结果正确的是（ ）
A．﹣2x2y22xy=﹣2x3y4
B．28x4y2÷7x3y=4xy
C．3x2y﹣5xy2=﹣2x2y
D．（﹣3a﹣2）（3a﹣2）=9a2﹣4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF=90°，且EF交正方形的外角∠DCM的平分线CF于点F．
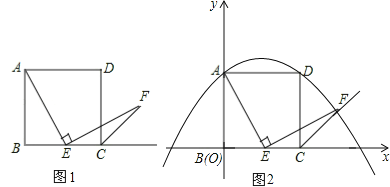
（1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；
（2）如图2，若点E在线段BC上滑动（不与点B，C重合）．
①AE=EF是否一定成立？说出你的理由；
②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点，当点E滑动到某处时，点F恰好落在此抛物线上，求此时点F的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把8a3－8a2＋2a进行因式分解，结果正确的是( )
A. 2a(4a2－4a＋1) B. 8a2(a－1)
C. 2a(2a＋1)2 D. 2a(2a－1)2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】低碳生活备受关注．小明为了了解人们到某超市购物时使用购物袋的情况，利用星期日到该超市对部分购物者进行调查，并把调查结果绘制成两幅不完整的统计图．假设当天每人每次购物时都只用一个环保购物袋（可降解）或塑料购物袋（不可降解）．
A．一自备环保购物袋
B．一自备塑料购物袋
C．一购买环保购物袋
D．一购买塑料购物袋
根据以上信息，回答下列问题：
（1）小明这次调查到的购物人数是 人次；
（2）补全两幅统计图；
（3）若当天到该超市购物者共有2000人次，请你估计该天使用环保购物袋有 人次，使用塑料购物袋有 人次；
（4）在大力倡导低碳生活的今天，你认为在购物时应尽量使用 购物袋．（填“环保”或“塑料”）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作ABDE，连接AD，EC．
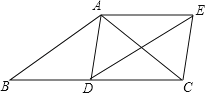
（1）求证：△ADC≌△ECD；
（2）若BD=CD，求证：四边形ADCE是矩形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com