
����Ŀ����ͼ1����֪������ABCD�ı߳�Ϊ1����E�ڱ�BC�ϣ�����AEF=90������EF�������ε������DCM��ƽ����CF�ڵ�F��
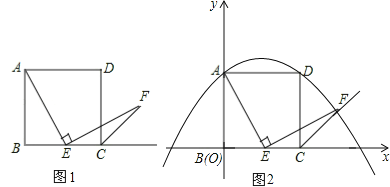
��1��ͼ1������E�DZ�BC���е㣬���ǿ��Թ�������������ȫ����֤��AE=EF�����������һ�����췽������ָ����������������ȫ�ȣ���Ҫ��֤������
��2����ͼ2������E���߶�BC�ϻ����������B��C�غϣ���
��AE=EF�Ƿ�һ��������˵��������ɣ�
������ͼ2��ʾ��ֱ������ϵ��������y=ax2+x+c����A��D���㣬����E������ij��ʱ����Fǡ�����ڴ��������ϣ����ʱ��F�����꣮
���𰸡���1������������2�������������ڵ�F������ΪF��![]() ��
��![]() ��
��
��������
�����������1��������AEF=90��������FEC=��EAB����E��BC�е㣬�Ӷ�ֻ��ȡAB��G������EG������AG=CE��BG=BE����AGE=��ECF������AGE�ա�ECF��
��2��������AB=BC������ֻҪAG=EC����BG=BE����ͬ���ɵ���AGE�ա�ECF�����ǽ�ȡAG=EC��֤ȫ�ȼ��ɣ�
�ڸ���A��D�����������������߽���ʽ�����F��ĺ����꣬�������ú������ʾ����F���������������߽���ʽ����������꣮
�⣺��1����ͼ1��ȡAB���е�G������EG����AGE�ա�ECF��
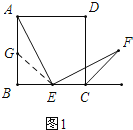
��2��������E���߶�BC�ϻ���ʱAE=EF�ܳ�����
֤������ͼ2����AB�Ͻ�ȡAG=EC��
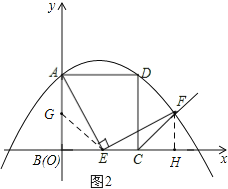
��AB=BC��
��BG=BE��
���GBE�ǵ���ֱ�������Σ�
���AGE=180����45��=135�㣬
��CFƽ�������ε���ǣ�
���ECF=135����
���AGE=��ECF��
����BAE+��AEB=��CEF+��AEB=90����
���BAE=��CEF��
���AGE�ա�ECF��
��AE=EF��
���������֪�����߾���A��0��1����D��1��1�����㣬
��![]() �����
�����![]() ��
��
�������߽���ʽΪy=��x2+x+1��
����F��FH��x����H��
�ɢ�֪��FH=BE=CH����BH=a����FH=a��1��
����F������ΪF��a��a��1����
����Fǡ������������y=��x2+x+1�ϣ�
��a��1=��a2+a+1��
��a=![]() ����ֵ�������⣬��ȥ����
����ֵ�������⣬��ȥ����
��F������ΪF��![]() ��
��![]() ��.
��.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ж������г��ļ��������������ε�֧�ܣ�������Ϊ�����ξ���_______��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ�٣�ABCD�ĶԽ���AC��BD���ڵ�O��ֱ��EF����O���ֱ�AD��BC�ڵ�E��F����֤��AE=CF��
��2����ͼ�ڣ���ABCD��ֽƬ���ع��Խ��߽���O��ֱ��EF�۵�����A���ڵ�A1������B���ڵ�B1������FB1��CD�ڵ�G��A1B1�ֱ�CD��DE�ڵ�H��I����֤��EI=FG��
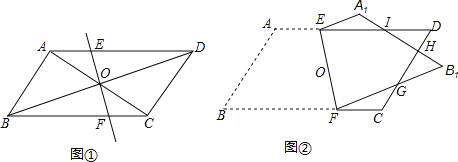
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѷ���2x��x��3��=3x+2����һԪ���η��̵�һ����ʽ������һ����ϵ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ�
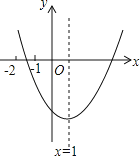
��b2��4ac��0��
��abc��0��
�۵�x��0ʱ��y��x�����������
��9a+3b+c��0��
���У���ȷ������ �������������ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x2=x�Ľ��ǣ� ��
A��x=1 B��x1=��1��x2=1 C��x1=0��x2=1 D��x=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��kx��6=0��һ����Ϊx=3����ʵ��k��ֵΪ�� ��
A��1 B����1 C��2 D����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��0��0����A��0��1����������OAA1B���������㣬��OA1�Խ���Ϊ����������OA1A2B1�����������εĶԽ���OA2��������OA1A2B1���������˹��ɣ����A8�������ǣ� ��
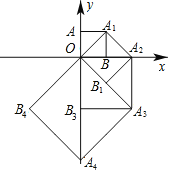
A������8��0�� B����0��8�� C����0��8![]() �� D����0��16��
�� D����0��16��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com