
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据抛物线与x轴的交点问题可判断抛物线y=ax2-2x+1与x轴没有交点,由c=1>0可判断抛物线与y轴的交点在x轴上方,所以抛物线的开口向上,则a>0,接着判断抛物线的对称轴在y轴的右侧,从而确定抛物线y=ax2-2x+1的顶点所在象限.
解答 解:∵一元二次方程ax2-2x+1=0没有实数根,
∴a≠0且△<0,
∴抛物线y=ax2-2x+1与x轴没有交点,
而c=1>0,
∴抛物线与y轴的交点在x轴上方,
∴抛物线的开口向上,
∴a>0,
而抛物线的对称轴为直线x=-$\frac{-2}{2a}$=$\frac{1}{a}$,
∴抛物线的对称轴在y轴的右侧,
∴抛物线y=ax2-2x+1的顶点在第一象限.
故选A.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
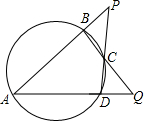 如图,点A、B、C,D在同一圆上,AD,BC延长线相交于点Q,AB,DC的延长线相交于点P.若∠A=50°,∠P=35°,则∠Q=45°.
如图,点A、B、C,D在同一圆上,AD,BC延长线相交于点Q,AB,DC的延长线相交于点P.若∠A=50°,∠P=35°,则∠Q=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
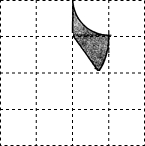 如图,已知网格中每个小正方形的边长都是1,图中的图案由两段以格点为圆心,分别以1和2为半径的圆弧和网格的边围成.
如图,已知网格中每个小正方形的边长都是1,图中的图案由两段以格点为圆心,分别以1和2为半径的圆弧和网格的边围成.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
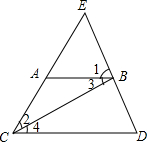 如图,下列推理所注的依据正确的是(3)(填序号)
如图,下列推理所注的依据正确的是(3)(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
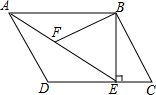 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/个) | 10 | 11 | 12 | 13 | … |
| 每周销量(个) | 20 | 18 | 16 | 14 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=-1 | B. | m=1 | C. | m=2 | D. | 无法确定m的值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com