
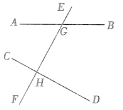
【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=![]() ∠AGE.
∠AGE.
(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
【答案】(1)CD⊥EF;(2) ∠CHG的同位角∠AGE=120°,内错角∠BGF=∠AGE=120°,同旁内角∠AGF=60°
【解析】
(1)先由∠CHG+∠DHG=180°及∠CHG=∠DHG,可得∠CHG=∠DHG =90°,再根据垂直的定义得到CD与EF互相垂直;
(2)先由∠CHG=∠DHG =![]() ∠AGE,可得∠AGE=120°,再根据同位角、内错角、同旁内角的定义即可求解.
∠AGE,可得∠AGE=120°,再根据同位角、内错角、同旁内角的定义即可求解.
(1)CD⊥EF.理由如下:
因为CD是直线,所以∠CHG+∠DHG=180°,
又∠CHG=∠DHG,所以∠CHG=∠DHG=90°,
所以CD⊥EF.
(2)由(1)知∠CHG=∠DHG=90°,
因为∠CHG=∠DHG=![]() ∠AGE,
∠AGE,
所以∠AGE=120°,
所以∠CHG的同位角∠AGE=120°,内错角∠BGF=∠AGE=120°,同旁内角∠AGF=180°-∠AGE=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速
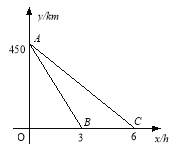
运动.快车离乙地的路程y1 (km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示.慢车离甲地的路
程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段AC所示.根据图像进行以下研究.
解读信息:(1)甲、乙两地之间的距离为 km;
(2)线段AB的解析式为 ; 两车在慢车出发 小时后相遇;
问题解决:
(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新化到长沙的距离约为200km,小王开着小轿车,张师傅开着大货车都从新化去长沙,小王比张师傅晚出发20分钟,最后两车同时到达长沙.已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
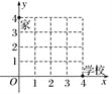
A. (0,4)→(0,0)→(4,0)
B. (0,4)→(4,4)→(4,0)
C. (0,4)→(3,4)→(4,2)→(4,0)
D. (0,4)→(1,4)→(1,1)→(4,1)→(4,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
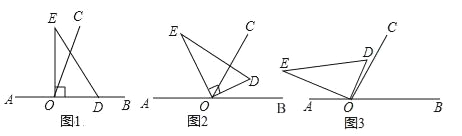
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,边 AC,BC 的垂直平分线的交点 O 落在边 AB 上,则△ABC 的形状是( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 任意三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
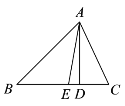
【题目】如图,在△ABC 中,∠C=65°,AD 为 BC 边上的高.
(1)求∠CAD 的度数;
(2)若∠B=45°,AE 平分∠BAC,求∠EAD 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com