
【题目】已知,![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() .
.

(1)如图 1,若![]() ,求
,求![]() 的度数;
的度数;
(2)把“![]() °”改为“
°”改为“![]() ”,射线
”,射线![]() 沿射线
沿射线![]() 平移,得到
平移,得到![]() ,其它条件不变(如 图 2 所示),探究
,其它条件不变(如 图 2 所示),探究![]() 的数量关系;
的数量关系;
(3)在(2)的条件下,作![]() ,垂足为
,垂足为![]() ,与
,与![]() 的角平分线
的角平分线![]() 交于点
交于点![]() ,若
,若![]() , 用含 α 的式子表示
, 用含 α 的式子表示![]() (直接写出答案).
(直接写出答案).
【答案】(1) 150°;(2) ∠OCD+∠BO'E=240°;(3) 30°+![]() .
.
【解析】
(1)先求出到∠AOE的度数,再根据直角、周角的定义即可求解;
(2)过O点作OF//CD,根据平行线的判定和性质可得∠OCD、∠BO'E的数量关系;
(3)根据四边形内角和为360°,再结合(2)的结论以及角平分线的定义即可解答.
解:(1)∵CD//OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°-90°-120°=150°;
(2)如图2,过O点作OF//CD,
∴CD//OE,
∴OF∥OE,
∴∠AOF=180°-∠OCD,∠BOF=∠EO'O=180°-∠BO'E,
∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO'E=360°-(∠OCD+∠BO'E)=120°,
∴∠OCD+∠BO'E=240°;
(3)∵CP是∠OCD的平分线,
∴∠OCP=![]() ∠OCD,
∠OCD,
∴∠CPO'=360°-90°-120°-∠OCP
=150°-![]() ∠OCD
∠OCD
=150°-![]() (240°-∠BO'E)
(240°-∠BO'E)
=30°+![]()



科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
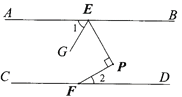
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:![]() ;
;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市2016年中考,综合素质测试满分为100分.某校为了调查学生对于综合素质的掌握程度,在九年级学生中随机抽取了部分学生进行模拟测试,并将测试成绩绘制成下面两幅统计图.
试根据统计图中提供的数据,回答下面问题:
(1)计算样本中,成绩为98分的学生有分,并补全条形统计图.
(2)样本中,测试成绩的中位数是分,众数是分.
(3)若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合速度测试将有多少名学生可以获得满分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图(1),连接AF、CE.
①四边形AFCE是什么特殊四边形?说明理由;
②求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板的三个内角分别是90![]() ,45
,45![]() ,45
,45![]() 和90
和90![]() ,60
,60![]() ,30
,30![]() ,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0
,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0![]() <α<180
<α<180![]() )
)
(1)如图1中,请你探索当α为多少时,CD∥OB,并说明理由;
(2)如图2中,当α=___时,AD∥OB;
(3)在点A位置始终不变的情况下,你还能摆成几种不同的位置,使两块三角板中至少有一组边平行,请直接写出符合要求的α的度数。(写出三个即可)
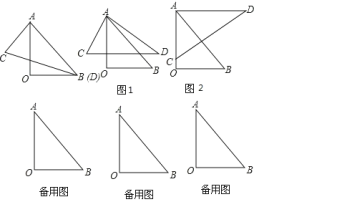
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com