
| 13 |
| 6 |
|
|
| 2 |
| 3 |
| 10 |
| 3 |
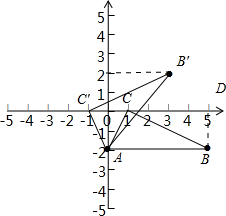 ,
,
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 2 |
| 3 |
| 13 |
| 6 |
| 2 |
| 3 |
| 13 |
| 3 |


科目:初中数学 来源: 题型:
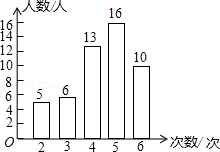 (1)某市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题;
(1)某市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
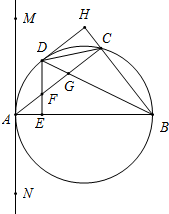 如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、点A在⊙C内 |
| B、点A在⊙C上 |
| C、点A在⊙C外 |
| D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
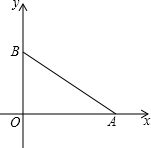 如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.
如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com