
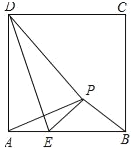
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
【答案】1或![]()
【解析】
分两种情况讨论:若AP=BP时,△ADP是等边三角形;若AP=AB时,点P在AB的垂直平分线上,且PF⊥AD,得到PF=![]() AB,在理折叠的性质和正方形性质即可解答
AB,在理折叠的性质和正方形性质即可解答
若AP=BP,
∵四边形ABCD是正方形
∴AD=AB,∠DAB=90°,
∵折叠
∴AD=DP=AP,∠ADE=∠PDE
∴△ADP是等边三角形
∴∠ADP=60°
∴∠ADE=30°
∴AE=![]() =
=![]()
若AP=AB,
如图,过点P作PF⊥AD于点F,作∠MED=∠MDE,
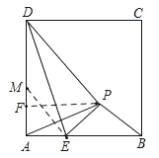
∵AP=PB,
∴点P在AB的垂直平分线上,且PF⊥AD,
∴PF=![]() AB,
AB,
∵折叠
∴AD=DP=AB,∠ADE=∠PDE
∴PF=![]() PD
PD
∴∠PDF=30°
∴∠ADE=15°
∵∠MED=∠MDE,
∴∠AME=30°,ME=MD
∴AM=![]() AE,ME=2AE
AE,ME=2AE
∴AD=2AE+![]() AE=2+
AE=2+![]()
∴AE=1
故答案为1或 ![]()


科目:初中数学 来源: 题型:
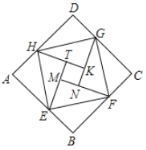
【题目】汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们利用“公众号”进行学习和获取信息已成为了生活常态,为了解某个学习类公众号的推广情况,小方同学调查统计了从周一到周五对该公众号进行关注的“粉丝”人数的变化情况,并将结果绘制成如图1和图2所示的两个不完整的统计图

根据以上信息,完成下面的问题:
(1)如图2,周三进行关注的“粉丝”人数对应的扇形圆心角是 °;
(2)将折线统计图补充完整;
(3)在原来基础上,小方对该公众号又统计了后续周六和周日关注的“粉丝”人数发现这7天平均每天关注的“粉丝”人数比前5天平均每天关注的“粉丝”人数多2人,则
①周六和周日这两天关注了该公众号的一共是 人;
②现从周六关注公众号的前3位男士“粉丝”和周日关注公众号的前2位女士“粉丝”中,随机抽取两位进行奖励,请用列表法或者画树状图的方法,求所抽取的两位“粉丝”恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类: ![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.
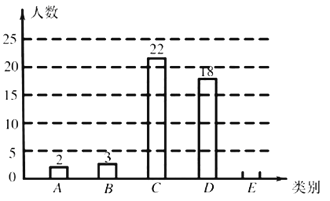
根据以上信息,解答下列问题:
(1)![]() 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=2,点E是BC边的中点,连接AE,△AB′E和△ABE关于AE所在直线对称,若△B′CD是直角三角形,则BC边的长为_____.
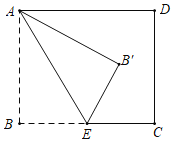
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为24元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于32元件,市场调查发现,该产品每天的销售最![]() (件)与
(件)与![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
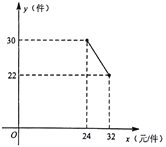
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元/件)之问的函数关系式并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之问的函数关系式并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y轴交于点c直线y=﹣x+4经过点B、C.
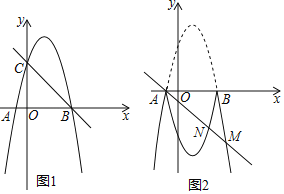
(1)求抛物线的表达式;
(2)过点A的直线y=kx+k交抛物线于点M,交直线BC于点N,连接AC,当直线y=kx+k平分△ABC的面积,求点M的坐标;
(3)如图2,把抛物线位于x轴上方的图象沿x轴翻折,当直线y=kx+k与翻折后的整个图象只有三个交点时,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com