
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类: ![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.
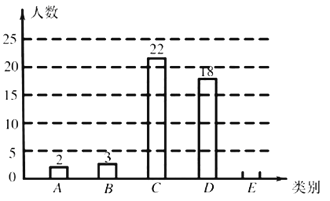
根据以上信息,解答下列问题:
(1)![]() 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
科目:初中数学 来源: 题型:
【题目】矩形Ⅰ的面积为6,矩形Ⅱ中的三条边总长为6,则下列说法不正确的是( )
A.矩形Ⅰ中一组邻边的长满足反比例函数关系
B.矩形Ⅰ中一组邻边的长可能是3+![]() 和3﹣
和3﹣![]()
C.矩形Ⅰ的周长不可能是8
D.矩形Ⅱ的最大面积是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
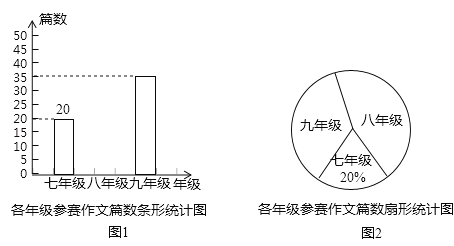
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=![]() (k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
(k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
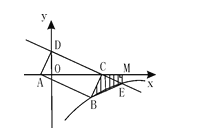
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
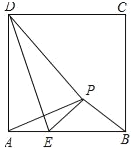
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰2个白色小正方形(每个白色小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰2个白色小正方形(每个白色小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com