
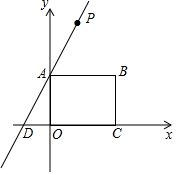
 如图,在直角坐标系中,矩形OABC的两边在坐标轴上,其中点B的坐标为(4,3),过点A的直线AD的解析式为y=2x+3,点P是直线AD上一动点,以P,B,C为顶点作平行四边形PBEC,当对角线PE的值最小时,求点P的坐标.
如图,在直角坐标系中,矩形OABC的两边在坐标轴上,其中点B的坐标为(4,3),过点A的直线AD的解析式为y=2x+3,点P是直线AD上一动点,以P,B,C为顶点作平行四边形PBEC,当对角线PE的值最小时,求点P的坐标. 分析 首先连接PE交BC于点M,判断出当MP⊥AD时,MP的值最小;然后应用点斜式,求出直线PE的解析式;最后求出直线AD、直线PE的交点P的坐标是多少即可.
解答 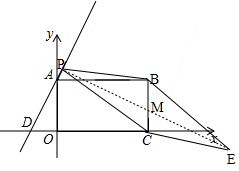 解:如图,连接PE交BC于点M,
解:如图,连接PE交BC于点M,
∵四边形PBEC是平行四边形,
∴PM=ME=$\frac{1}{2}$PE,
∴当MP⊥AD时,MP的值最小,
即PE⊥AD时,对角线PE的值最小,
∵直线AD的解析式为y=2x+3,且PE⊥AD,
∴直线PE的斜率为-$\frac{1}{2}$,
∴设直线PE的解析式为y=-$\frac{1}{2}$x+c,
∵四边形OABC是矩形,且点B的坐标为(4,3),点C的坐标为(4,0),
∴点M的坐标为(4,1.5),
∴-$\frac{1}{2}$×4+c=1.5,
解得c=3.5,
∴直线PE的解析式为y=-$\frac{1}{2}$x+3.5,
由$\left\{\begin{array}{l}{y=2x+3}\\{y=-\frac{1}{2}x+3.5}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1}{5}}\\{y=\frac{17}{5}}\end{array}\right.$
∴当对角线PE的值最小时,点P的坐标是($\frac{1}{5}$,$\frac{17}{5}$).
点评 此题主要考查了直线解析式的求法,一次函数图象上点的坐标特征,矩形的性质以及平行四边形的性质和应用,求得直线PE的解析式是解题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
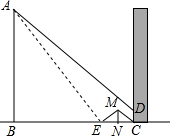 阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)
阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
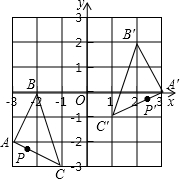 如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )
如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )| A. | (-m,n+2) | B. | (-m,n-2) | C. | (-m-2,-n) | D. | (-m-2,n-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
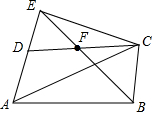 如图,在?ABCD中,∠ABC的平分线与AD的延长线交于点E,与CD交于点F,且点F是CD的中点,连结AC,CE.已知FC=3,FB=2$\sqrt{2}$,则△ACE的面积为4$\sqrt{14}$.
如图,在?ABCD中,∠ABC的平分线与AD的延长线交于点E,与CD交于点F,且点F是CD的中点,连结AC,CE.已知FC=3,FB=2$\sqrt{2}$,则△ACE的面积为4$\sqrt{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
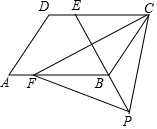 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
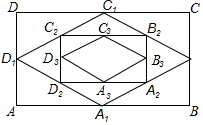 由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.
由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com