
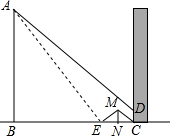
 �������ĵ�һ�죬С����С�������������Լ���ѧ֪ʶ����¥ǰ��˵ĸ߶ȣ�ijһʱ�����AB��Ӱ��һ�����ڵ����ϣ���һ��������ѧ¥��ǽ���ϸ߶ȼ�ΪCD��ͬһʱ��С�����ڵ���N����С����Ӱ�Ӹպõ���ǽ��C����С����С�������֮���ֱ��BN��ƽ��һƽ�澵���������ϵ�����ֱ��С�����ھ����п�����˵Ķ�������ƽ�澵��λ��ΪE������ƽ�澵�ĸ߶ȣ���С�����ŵĸ߶ȼ�ΪMN���������絽ͷ���ľ��룩����С�����ڵ����ϵĸ߶�һֱ���ֲ��䣬��ʱС����BE=12.51�ף�EN=1.09�ף�NC=1.4�ף�CD=1�ף�����˵ĸ߶ȣ��������ȷ��0.1�ף�
�������ĵ�һ�죬С����С�������������Լ���ѧ֪ʶ����¥ǰ��˵ĸ߶ȣ�ijһʱ�����AB��Ӱ��һ�����ڵ����ϣ���һ��������ѧ¥��ǽ���ϸ߶ȼ�ΪCD��ͬһʱ��С�����ڵ���N����С����Ӱ�Ӹպõ���ǽ��C����С����С�������֮���ֱ��BN��ƽ��һƽ�澵���������ϵ�����ֱ��С�����ھ����п�����˵Ķ�������ƽ�澵��λ��ΪE������ƽ�澵�ĸ߶ȣ���С�����ŵĸ߶ȼ�ΪMN���������絽ͷ���ľ��룩����С�����ڵ����ϵĸ߶�һֱ���ֲ��䣬��ʱС����BE=12.51�ף�EN=1.09�ף�NC=1.4�ף�CD=1�ף�����˵ĸ߶ȣ��������ȷ��0.1�ף� ���� ��ͼ���ӳ�AD��BC��H����AB=x��MN=y��CH=z���������������ε����ʣ���ߣ�Ӱ��=��ߣ�Ӱ�����г���Ԫ�����飬���ɽ�����⣮
��� �⣺��ͼ���ӳ�AD��BC��H����AB=x��MN=y��CH=z��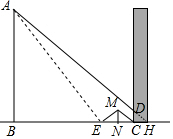
�������֪$\left\{\begin{array}{l}{\frac{x}{y}=\frac{12.51}{1.09}}\\{\frac{y}{1.4}=\frac{1}{z}}\\{\frac{x}{12.51+1.09+1.4+z}=\frac{y}{1.4}}\end{array}\right.$���$\left\{\begin{array}{l}{x=15.0}\\{y=1.3}\\{z=1.1}\end{array}\right.$��
����˵ĸ߶�Ϊ15.0�ף�
���� ���⿼�����������ε����ʣ�����Ĺؼ�����������ǵ��ڷ���ǣ�������ߣ�Ӱ��=��ߣ�Ӱ���������п��������ͣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
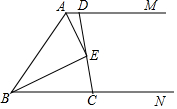 ��ͼ��AM��BN����MAB�͡�NBA��ƽ���߽���E�㣮��
��ͼ��AM��BN����MAB�͡�NBA��ƽ���߽���E�㣮���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
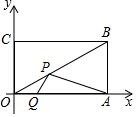 ��֪��ƽ��ֱ������ϵ�У�����OABC�Ķ���OΪ����ԭ�㣬����A��B������ֱ�Ϊ��20��0������20��10����P��Q�ֱ�Ϊ�߶�OB��OA�ϵĶ��㣬��PQ+PA��Сʱ����P������Ϊ��12��6����
��֪��ƽ��ֱ������ϵ�У�����OABC�Ķ���OΪ����ԭ�㣬����A��B������ֱ�Ϊ��20��0������20��10����P��Q�ֱ�Ϊ�߶�OB��OA�ϵĶ��㣬��PQ+PA��Сʱ����P������Ϊ��12��6�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
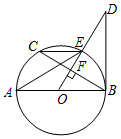 ��ͼ��AB�ǡ�Oֱ����OD����BC�ڵ�F���ҽ���O�ڵ�E���ҡ�AEC=��ODB��
��ͼ��AB�ǡ�Oֱ����OD����BC�ڵ�F���ҽ���O�ڵ�E���ҡ�AEC=��ODB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
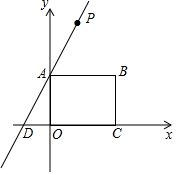 ��ͼ����ֱ������ϵ�У�����OABC���������������ϣ����е�B������Ϊ��4��3��������A��ֱ��AD�Ľ���ʽΪy=2x+3����P��ֱ��AD��һ���㣬��P��B��CΪ������ƽ���ı���PBEC�����Խ���PE��ֵ��Сʱ�����P�����꣮
��ͼ����ֱ������ϵ�У�����OABC���������������ϣ����е�B������Ϊ��4��3��������A��ֱ��AD�Ľ���ʽΪy=2x+3����P��ֱ��AD��һ���㣬��P��B��CΪ������ƽ���ı���PBEC�����Խ���PE��ֵ��Сʱ�����P�����꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 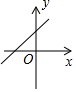 | B�� | 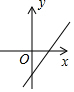 | C�� | 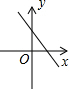 | D�� | 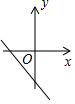 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
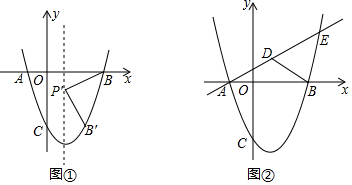
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com