
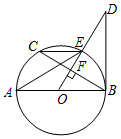
 如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.分析 (1)由∠AEC=∠ODB、∠AEC=∠ABC知∠ABC=∠ODB,根据∠DBC+∠ODB=90°得∠DBC+∠ABC=90°,即可得证;
(2)由OD⊥BC、BC=8知FB=FC=4,根据tan∠AEC=tan∠ODB=tan∠OBF=$\frac{3}{4}$,求得DF=$\frac{16}{3}$,OF=3,据此可得答案.
解答 解:(1)直线BD和⊙O相切,
∵∠AEC=∠ODB,∠AEC=∠ABC,
∴∠ABC=∠ODB,
∵OD⊥BC,
∴∠DBC+∠ODB=90°,
∴∠DBC+∠ABC=90°,
∴∠DBO=90°,
∴直线BD和⊙O相切.
(2)∵OD⊥BC,BC=8,
∴FB=FC=4,
∵tan∠AEC=tan∠ODB=tan∠OBF=$\frac{3}{4}$,
∴$\frac{DF}{BF}$=$\frac{3}{4}$,$\frac{OF}{BF}$=$\frac{3}{4}$,
∴DF=$\frac{16}{3}$,OF=3,
∴OD=OF+DF=3+$\frac{16}{3}$=$\frac{25}{3}$.
点评 本题主要考查直线与圆的位置关系、圆周角定理、正切函数,熟练掌握切线的判定、圆周角定理及正切函数的定义是解题的关键.


科目:初中数学 来源: 题型:填空题
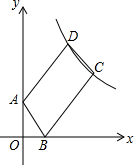 如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.
如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
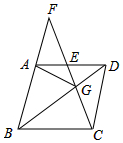 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
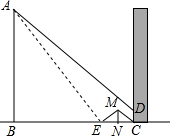 阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)
阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
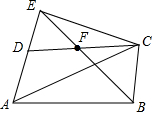 如图,在?ABCD中,∠ABC的平分线与AD的延长线交于点E,与CD交于点F,且点F是CD的中点,连结AC,CE.已知FC=3,FB=2$\sqrt{2}$,则△ACE的面积为4$\sqrt{14}$.
如图,在?ABCD中,∠ABC的平分线与AD的延长线交于点E,与CD交于点F,且点F是CD的中点,连结AC,CE.已知FC=3,FB=2$\sqrt{2}$,则△ACE的面积为4$\sqrt{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
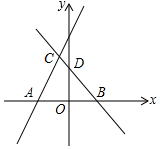 如图,直线y=2x+m(m>0)与x轴交于点A,直线y=-x+n(n>0)与x轴、y轴分别交于B、D,并与直线y=2x+m相交于点C,若AB=4,四边形CAOD的面积为$\frac{10}{3}$,求m、n的值.
如图,直线y=2x+m(m>0)与x轴交于点A,直线y=-x+n(n>0)与x轴、y轴分别交于B、D,并与直线y=2x+m相交于点C,若AB=4,四边形CAOD的面积为$\frac{10}{3}$,求m、n的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com