
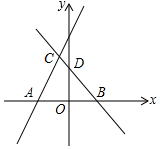
 如图,直线y=2x+m(m>0)与x轴交于点A,直线y=-x+n(n>0)与x轴、y轴分别交于B、D,并与直线y=2x+m相交于点C,若AB=4,四边形CAOD的面积为$\frac{10}{3}$,求m、n的值.
如图,直线y=2x+m(m>0)与x轴交于点A,直线y=-x+n(n>0)与x轴、y轴分别交于B、D,并与直线y=2x+m相交于点C,若AB=4,四边形CAOD的面积为$\frac{10}{3}$,求m、n的值. 分析 先根据函数解析式,求得交点C($\frac{n-m}{3}$,$\frac{2n+m}{3}$),A(-$\frac{1}{2}$m,0),B(n,0),D(0,n),再根据AB=4,四边形CAOD的面积为$\frac{10}{3}$,即可得到关于m,n的方程组,进而求得m、n的值.
解答  解:解方程组$\left\{\begin{array}{l}{y=2x+m}\\{y=-x+n}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=\frac{n-m}{3}}\\{y=\frac{2n+m}{3}}\end{array}\right.$,
解:解方程组$\left\{\begin{array}{l}{y=2x+m}\\{y=-x+n}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=\frac{n-m}{3}}\\{y=\frac{2n+m}{3}}\end{array}\right.$,
∴C($\frac{n-m}{3}$,$\frac{2n+m}{3}$),
在直线y=2x+m中,令y=0,则x=-$\frac{1}{2}$m,
∴A(-$\frac{1}{2}$m,0),
在直线y=-x+n中,令y=0,则x=n;令x=0,则y=n,
∴B(n,0),D(0,n),
∵AB=4,
∴n-(-$\frac{1}{2}$m)=4,①
∵四边形CAOD的面积为$\frac{10}{3}$,
∴△ABC的面积-△BDO的面积=$\frac{10}{3}$,
即$\frac{1}{2}$×4×$\frac{2n+m}{3}$-$\frac{1}{2}$n2=$\frac{10}{3}$,②
联立①②,解方程组可得
n=2,m=4.
点评 本题主要考查了两直线相交问题,解题时注意:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.


科目:初中数学 来源: 题型:选择题
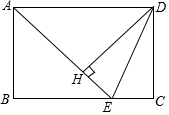 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
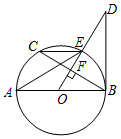 如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 计费项目 | 里程费 | 时长费 | 远途费 |
| 单价 | 1.8元/公里 | 0.3元/分钟 | 0.8元/公里 |
| 注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元. | |||
| A. | 10分钟 | B. | 13分钟 | C. | 15分钟 | D. | 19分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
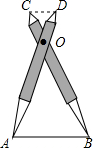 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )| A. | 12 | B. | 9 | C. | 8 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com