
| A. | 若∠C-∠B=∠A,则△ABC是直角三角形 | |
| B. | 若c2=b2-a2,则△ABC是直角三角形且∠C是直角 | |
| C. | 若(c+a)(c-a)=b2,则△ABC是直角三角形 | |
| D. | 若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形且∠A为直角 |
分析 根据三角形内角和定理求出最大角的度数,即可判断A与D;根据勾股定理的逆定理即可判断B与C.
解答 解:A、根据三角形内角和定理,可求出角C为90度,故△ABC是直角三角形,是真命题;
B、若c2=b2-a2,则b2=a2+c2,所以△ABC是直角三角形且∠B=90度,是假命题;
C、化简后有c2=a2+b2,根据勾股定理的逆定理,则△ABC是直角三角形,是真命题;
D、设三角分别为5x,2x,3x,根据三角形内角和定理可求得三个角分别为:90度,36度,54度,则△ABC是直角三角形,是真命题.
故选B.
点评 本题考查了直角三角形的判定.直角三角形的判定方法有:①求得一个角为90°,②利用勾股定理的逆定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
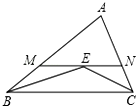 如图在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若AB+AC=7cm,则△AMN的周长为7cm.
如图在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若AB+AC=7cm,则△AMN的周长为7cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不带根号的数不是无理数 | B. | 8的立方根是±2 | ||
| C. | 绝对值是$\sqrt{5}$的实数是$\sqrt{5}$ | D. | 每个实数都对应数轴上对一个点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}\sqrt{3}=\sqrt{6}$ | B. | 3$\sqrt{5}-\sqrt{5}=2$ | C. | $\sqrt{18}÷\sqrt{2}=3$ | D. | (1+$\sqrt{2}$)2=$3+2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com