Question

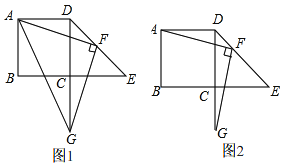
【题目】在正方形中，点在的延长线上，且，点为边上一点，连接，作交直线于点．

（1）如图1，填空：_____________；

（2）如图1，连接，若，求的面积；

（3）如图2，若时，求证：DG=+AD．

Answer 1

【答案】（1）135°；（2）20；（3）见解析

【解析】

（1）根据题意得出∠ADC=90°，∠CDE=45°，即可得出结果；

（2）先判断出∠ADF=∠GCF，进而得出△ADF≌△GCF，可得△AFG是等腰直角三角形，过F作FH⊥AD，交AD延长线于H，利用勾股定理和等腰三角形的性质求出AF和FG，即可得到△AFG的面积；

（3）过点F作FM⊥DE，证明△ADF≌△GMF，得出AD=MG，最后用等量代换即可得到结果．

解：（1）∵四边形ABCD为正方形，

∴∠ADC=∠DCB=∠DCE=90°，

∵CE=CD，

∴∠CDE=∠CED=45°，

∴∠ADE=90°+45°=135°；

（2）如图1，连接CF，
在Rt△CDE中，CE=CD，DF=EF，
∴CF=DF=EF，∠ECF=∠CDE=45°，

∴∠FCG=∠GCE+∠ECF=135°，
∴∠ADF=∠GCF=135°，
∵AF⊥FG，CF⊥DE，
∴∠AFG=∠DFC=90°，
∴∠AFD=∠GFC，
在△ADF和△GCF中，

，

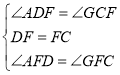∴△ADF≌△GCF（ASA），
∴AF=FG，
∵∠AFG=90°，
∴△AFG是等腰直角三角形，

过F作FH⊥AD，交AD延长线于H，

可知∠FDH=45°，即△FDH为等腰直角三角形，

设HF=DH=x，

∵AD=4=CD，

∴DE=，

∴DF=，

∴，

解得x=2，即DH=HF=2，AH=6，

∴在△AFH中，

AF==FG，

∴S△AFG==20；

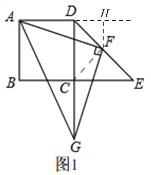
（3）如图2，过点F作FM⊥DE，

由（1）知，∠CDE=45°，

∴△DFM为等腰直角三角形，

∴DM=DF，DF=MF，∠DMF=45°，

∴∠GMF=135°=∠ADF，

∵MF⊥DE，

∴∠DFM=90°，

又∵∠AFG=90°，

∴∠AFD=∠GFM，

在△ADF和△GMF中，

，

∴△ADF≌△GMF（ASA），
∴AD=MG，
∴DG=DM+MG=DF+AD．