练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．设$\frac{4x-9}{3{x}^{2}-x-2}$=$\frac{A}{3x+2}$-$\frac{B}{x-1}$（A、B为常数），求A、B的值．

    分析 先把等式右边的分式通分，再令等式两边的分子相等即可得出A、B的值．

    解答 解：右边=$\frac{A（x-1）-B（3x+2）}{（3x+2）（x-1）}$=$\frac{（A-3B）x-（A+2B）}{3{x}^{2}-x-2}$，
    ∵分式两边的等式相等，
    ∴4x-9=（A-3B）x-（A+2B），
    ∴$\left\{\begin{array}{l}{A-3B=4}\\{A+2B=9}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{A=7}\\{B=1}\end{array}\right.$．

    点评 本题考查的是分式的加减法，在解答此题问题时要注意通分的灵活应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．一副三角尺按如图所示方式放置，试求∠AGF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．解方程：（2y-5）2=（3y-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

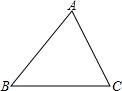    10．如图，在△ABC中，画出它们的三条中线AD、BE、CF，三条中线交于一点G，AG与GD的长度有什么关系？用刻度尺验证你的结论，换一个三角形试试看，上述结论是否还成立？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：
    （1）$\frac{5c}{6{a}^{2}b}$+$\frac{7a}{8{b}^{2}c}$-$\frac{b}{12{a}^{2}c}$；
    （2）$\frac{3}{x+2}$+$\frac{1}{2-x}$+$\frac{2x}{{x}^{2}-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，P是△ABC内一点，试说明2（PA+PB+PC）＞（AB+BC+AC）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

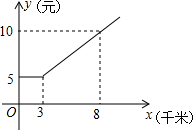    14．某歌唱大赛已经拉开序幕，欢欢准备乘坐出租车去比赛现场观看比赛，如图是乘坐出租车费用y（元）与路程x（千米）之间的函数图象．
    （1）请你说出该出租车的计费方法；
    （2）如果欢欢离比赛现场有15千米，那么他应付多少元车费？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．解方程：|x2+x|-12=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，在菱形ABCD中，AB=5，∠B：∠BCD=1：2，则对角线AC等于（　　）
    A．5B．10C．15D．20

    查看答案和解析>>

    同步练习册答案