
【题目】如图,在△ABC中,AB=AC.
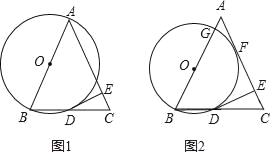
(1)如图1,若O为AB的中点,以O为圆心,OB为半径作⊙O交BC于点D,过D作DE⊥AC,垂足为E.
①试说明:BD=CD;
②判断直线DE与⊙O的位置关系,并说明理由.
(2)如图2,若点O沿OB向点B移动,以O为圆心,以OB为半径作⊙O与AC相切于点F,与AB相交于点G,与BC相交于点D,DE⊥AC,垂足为E,已知⊙O的半径长为4,CE=2,求切线AF的长.
【答案】(1)①证明见解析;②直线DE与⊙O相切,理由见解析;(2)AF=3.
【解析】
(1)①连接AD,已知AB是⊙O的直径,根据直径所对的圆周角是直角即可得∠ADB=90°,即AD⊥BC;再由等腰三角形三线合一的性质即可证得结论;(2)直线DE与⊙O相切,连接OD,已知AB=AC、OB=OD,根据等腰三角形的性质可得∠ODB=∠B=∠C,即可判定OD∥BC,由DE⊥AC可得DE⊥OD,由此即可判定DE与⊙O相切;(2)根据已知条件易证四边形ODEF是矩形,即可得OD=EF=4;设AF=x,则AB=AC=x+6,AO =x+2,在Rt△AOF中,利用勾股定理列出方程(x+2)2=x2+42,解方程求得x的值,即可求得AF的长.
(1)①连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,AD⊥BC,
∴BD=CD;
②直线DE与⊙O相切,
理由:连接OD,

∵AB=AC,OB=OD,
∴∠ODB=∠B=∠C,
∴OD∥BC,
∵DE⊥AC,
∴DE⊥OD,
∴DE与⊙O相切;
(2)由(1)同理得,DE与⊙O相切,
连接OF,
∵EF与⊙O相切,DE⊥AC,
∴∠ODE=∠OFE=∠EDF=90°,即四边形ODEF是矩形,
∴OD=EF=4,
设AF=x,则AB=AC=x+6,AO=x+6﹣4=x+2,
在Rt△AOF中,
(x+2)2=x2+42,
解得,x=3,
即AF=3.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2+(3–2m)x+m–2(m≠0)与x轴有两个不同的交点.
(1)求m的取值范围;
(2)判断点P(1,1)是否在抛物线上;
(3)当m=1时,求抛物线的顶点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
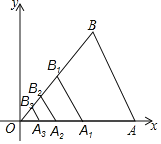
【题目】如图,在平面直角标系xOy中,以O为位似中心,将边长为8的等边三角形OAB作n次位似变换,经第一次变换后得到等边三角形OA1B1,其边长OA1缩小为OA的![]() ,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的
,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的![]() ,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的
,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的![]() ,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(
,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(![]() ,0),则n的值是( )
,0),则n的值是( )
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
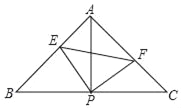
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:
①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;
④EF=AP.上述结论正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是甲、乙两种机器人根据电脑程序工作时各自工作量y关于工作时间x的函数图像,线段OA表示甲机器人的工作量![]() (吨)关于时间x(时)的函数图像,线段BC表示乙机器人的工作量
(吨)关于时间x(时)的函数图像,线段BC表示乙机器人的工作量![]() (吨)关于时间x(时)的函数图像.根据图像信息回答下列填空题.
(吨)关于时间x(时)的函数图像.根据图像信息回答下列填空题.
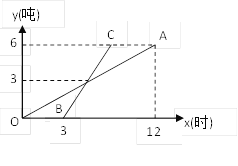
(1)甲种机器人比乙种机器人早开始工作 小时;甲种机器人每小时的工作量是 吨;
(2)直线BC的表达式为 ;当乙种机器人工作5小时后,它完成的工作量是 吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 是
是![]() 外一点,过点
外一点,过点![]() 做
做![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .若
.若![]() ,则点
,则点![]() 叫做
叫做![]() 的切角点.
的切角点.
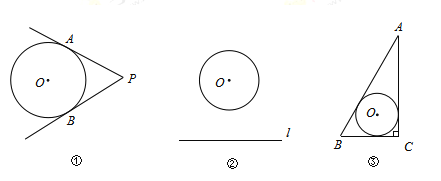
(1)如图②,![]() 的半径是1,点O到直线
的半径是1,点O到直线![]() 的距离为2.若点
的距离为2.若点![]() 是
是![]() 的切角点,且点
的切角点,且点![]() 在直线
在直线![]() 上,请用尺规作出点
上,请用尺规作出点![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的内切圆.若点
的内切圆.若点![]() 是
是![]() 的切角点,且点
的切角点,且点![]() 在
在![]() 的边上,求
的边上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com