
【题目】已知抛物线y=mx2+(3–2m)x+m–2(m≠0)与x轴有两个不同的交点.
(1)求m的取值范围;
(2)判断点P(1,1)是否在抛物线上;
(3)当m=1时,求抛物线的顶点Q的坐标.
【答案】(1)m<![]() 且m≠0;(2)点P(1,1)在抛物线上;(3)抛物线的顶点Q的坐标为(–
且m≠0;(2)点P(1,1)在抛物线上;(3)抛物线的顶点Q的坐标为(–![]() ,–
,–![]() ).
).
【解析】
(1)与x轴有两个不同的交点即令y=0,得到的一元二次方程的判别式△>0,据此即可得到不等式求解;
(2)把点(1,1)代入函数解析式判断是否成立即可;
(3)首先求得函数解析式,化为顶点式,可求得顶点坐标.
(1)由题意得,(3–2m)2–4m(m–2)>0,m≠0,
解得,m<![]() 且m≠0;
且m≠0;
(2)当x=1时,mx2+(3–2m)x+m–2=m+(3–2m)+m–2=1,
∴点P(1,1)在抛物线上;
(3)当m=1时,函数解析式为:y=x2+x–1=(x+![]() )2–
)2–![]() ,
,
∴抛物线的顶点Q的坐标为(–![]() ,–
,–![]() ).
).


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
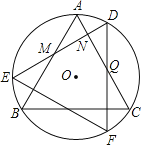
【题目】如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 .(把所有正确的结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
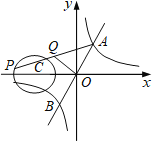
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文2张、数学1张、英语1张.
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率为______;
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率为______;
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______.
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
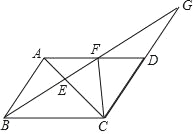
【题目】如图,AC是ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)若∠ABF=∠ACF,求证:CE2=EFEG;
(2)若DG=DC,BE=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
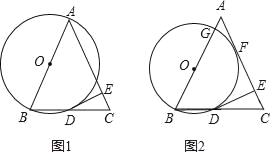
【题目】如图,在△ABC中,AB=AC.
(1)如图1,若O为AB的中点,以O为圆心,OB为半径作⊙O交BC于点D,过D作DE⊥AC,垂足为E.
①试说明:BD=CD;
②判断直线DE与⊙O的位置关系,并说明理由.
(2)如图2,若点O沿OB向点B移动,以O为圆心,以OB为半径作⊙O与AC相切于点F,与AB相交于点G,与BC相交于点D,DE⊥AC,垂足为E,已知⊙O的半径长为4,CE=2,求切线AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com