
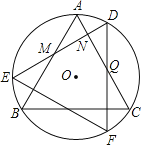
【题目】如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 .(把所有正确的结论的序号都填上)
【答案】①②③
【解析】
试题如图,连接OA、OD、OF、OC、DC、AD、CF,
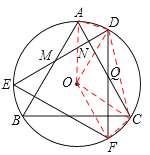
∵△ABC绕点O顺时针旋转30°得到△DEF,
∴∠AOD=∠COF=30°。
∴∠ACD=![]() ∠AOD=15°,∠FDC=
∠AOD=15°,∠FDC=![]() ∠COF=15°。
∠COF=15°。
∴∠DQN=∠QCD+∠QDC=15°+15°=30°。所以①正确。
同理可得∠AMN=30°。
∵△DEF为等边三角形,∴DE=DF。∴弧DE=弧DF。∴弧AE+弧AD=弧DC+弧CF。
∵弧AD=弧CF,∴弧AE=弧DC。∴∠ADE=∠DAC。∴ND=NA。
在△DNQ和△ANM中,∵∠DQN=∠AMN,∠DNQ=∠ANM,DN=AN。
∴△DNQ≌△ANM(AAS)。所以②正确。
∵∠ACD=15°,∠FDC=15°,∴QD=QC。
∵ND=NA,∴ND+QD+NQ=NA+QC+NQ=AC,即△DNQ的周长等于AC的长。所以③正确。
∵△DEF为等边三角形,∴∠NDQ=60°。
∵∠DQN=30°,∴∠DNQ=90°。∴QD>NQ。
∵QD=QC,∴QC>NQ。所以④错误。
综上所述,正确的结论是①②③。


科目:初中数学 来源: 题型:
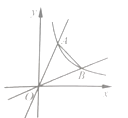
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生甲与乙学习概率初步知识后设计了如下游戏:甲手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,乙手中有
三张扑克牌,乙手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙一局比赛获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
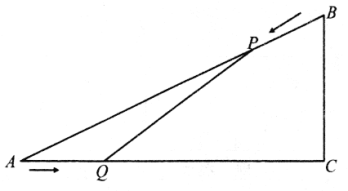
【题目】如图,已知![]() 中,
中,![]() cm,
cm,![]() cm,
cm,![]() cm.点
cm.点![]() 由
由![]() 出发,以5cm/s的速度沿
出发,以5cm/s的速度沿![]() 向点
向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由
由![]() 出发,以4cm/s的速度沿
出发,以4cm/s的速度沿![]() 向点
向点![]() 匀速运动.连接
匀速运动.连接![]() ,设运动时间为
,设运动时间为![]() (单位:
(单位:![]() ,
,![]() ).
).
(1)求点![]() 到
到![]() 的距离(用含
的距离(用含![]() 代数式表示);
代数式表示);
(2)求![]() 为何值时,线段
为何值时,线段![]() 将
将![]() 的面积分成的两部分的面积比为3∶13;
的面积分成的两部分的面积比为3∶13;
(3)当![]() 为直角三角形时,求
为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2+(3–2m)x+m–2(m≠0)与x轴有两个不同的交点.
(1)求m的取值范围;
(2)判断点P(1,1)是否在抛物线上;
(3)当m=1时,求抛物线的顶点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
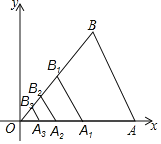
【题目】如图,在平面直角标系xOy中,以O为位似中心,将边长为8的等边三角形OAB作n次位似变换,经第一次变换后得到等边三角形OA1B1,其边长OA1缩小为OA的![]() ,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的
,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的![]() ,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的
,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的![]() ,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(
,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(![]() ,0),则n的值是( )
,0),则n的值是( )
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com