
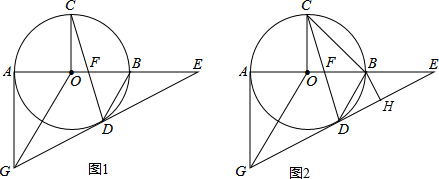
分析 (1)连接OD,由等腰三角形的性质和平行线的性质得出∠AOG=∠GOD,由SAS证明△AOG≌△DOG,得出对应边相等即可;
(2)由切线的性质得出∠OAG=90°,由全等三角形的性质得出∠OAG=∠ODG=90°,得出∠ODE=90°,∠ODC+∠FDE=90°,再由等腰三角形的性质和对顶角相等得出∠EFD=∠EDF,得出EF=ED即可;
(3)过点B作BK⊥OD于K,则∠OKB=∠BKD=∠ODE=90°,证明四边形KDHB为矩形,得出KD=BH=9,得出OK,由勾股定理求出KB,再由三角函数求出DE,得出EF,求出OF,由勾股定理求出FC,然后由勾股定理求出BC,即可得出△CBF的周长.
解答 (1)证明:连接OD,如图1所示: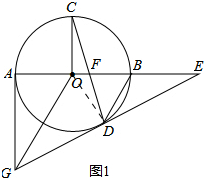
∵OB=OD,
∴∠ODB=∠OBD.
∵OG∥BD,
∴∠AOG=∠OBD,∠GOD=∠ODB,
∴∠AOG=∠GOD,
在△AOG和△DOG中,
$\left\{\begin{array}{l}{OA=OD}&{\;}\\{∠AOG=∠GOD}&{\;}\\{OG=OG}&{\;}\end{array}\right.$,
∴△AOG≌△DOG(SAS),
∴GD=GA;
(2)证明:∵AG切⊙O于A,
∴AG⊥OA,
∴∠OAG=90°,
∵△AOG≌△DOG,
∴∠OAG=∠ODG=90°,
∴∠ODE=180°-∠ODG=90°,
∴∠ODC+∠FDE=90°,
∵OC⊥AB,
∴∠COB=90°,
∴∠OCD+∠OFC=90°,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠FDE=∠OFC,
∵∠OFC=∠EFD,
∴∠EFD=∠EDF,
∴EF=ED,
∴△DEF是等腰三角形;
(3)解:过点B作BK⊥OD于K,如图2所示: 则∠OKB=∠BKD=∠ODE=90°,
则∠OKB=∠BKD=∠ODE=90°,
∴BK∥DE,
∴∠OBK=∠E,
∵BH⊥GE,
∴∠BHD=∠BHE=90°,
∴四边形KDHB为矩形,
∴KD=BH=9,
∴OK=OD-KD=$\frac{7}{2}$,
∵OK2+KB2=OB2,OB=$\frac{25}{2}$,
∴KB=12,
∴tan∠E=tan∠OBK=$\frac{OK}{KB}$=$\frac{7}{24}$,
sin∠E=sin∠OBK=$\frac{OK}{OB}$=$\frac{7}{25}$,
∵tan∠E=$\frac{OD}{DE}$=$\frac{7}{24}$,
∴DE=$\frac{300}{7}$,
∴EF=$\frac{300}{7}$,
∵sin∠E=$\frac{BH}{BE}$=$\frac{7}{25}$,
∴BE=$\frac{225}{7}$,
∴BF=EF-BE=$\frac{75}{7}$,
∴OF=OB-BF=$\frac{25}{14}$,
∵∠COB=90°,
∴OC2+OF2=FC2,
∴FC=$\frac{125\sqrt{2}}{14}$,
∵OC2+OB2=BC2,OC=OB=$\frac{25}{2}$,
∴BC=$\frac{25\sqrt{2}}{2}$,
∴BC+CF+BF=$\frac{150\sqrt{2}+75}{7}$,
∴△CBF的周长为=$\frac{150\sqrt{2}+75}{7}$.
点评 本题是圆的综合题目,考查了全等三角形的判定与性质、切线的性质、等腰三角形的判定与性质、矩形的判定与性质、三角函数、勾股定理等知识;本题综合性强,难度较大,特别是(3)中,需要通过作辅助线多次运用勾股定理和三角函数才能得出结果.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图:△ABC中,∠ACB=90°
已知如图:△ABC中,∠ACB=90°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
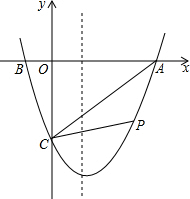 已知(如图所示):抛物线y=ax2+bx+c经过点A(3,0)、C(0,-3)其对称轴为x=1.
已知(如图所示):抛物线y=ax2+bx+c经过点A(3,0)、C(0,-3)其对称轴为x=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
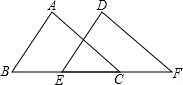 如图,在△ABC和△DEF中,∠A=∠D,AC=DF,若根据“ASA”说明△ABC≌△DEF,则应添加条件∠ACB=DFE.或AC∥DF.
如图,在△ABC和△DEF中,∠A=∠D,AC=DF,若根据“ASA”说明△ABC≌△DEF,则应添加条件∠ACB=DFE.或AC∥DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
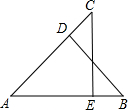 如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.
如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 西瓜种类 | A | B | C |
| 每辆汽车运载量(吨) | 4 | 5 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com