
)如图13,已知Rt△ACB中,∠C=90°,∠BAC=45°.
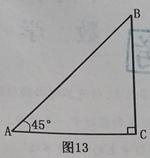
(1)(4分)用尺规作图,:在CA的延长线上截取AD=AB,并连接
BD(不写作法,保留作图痕迹)
(2)(4分)求∠BDC的度数.
(3)(4分)定义:在直角三角形中,一个锐角A的邻边与对边的比叫
做∠A的余切,记作cotA,即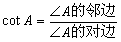 ,根据定义,利
,根据定义,利
用图形求cot22.5°的值.
科目:初中数学 来源: 题型:
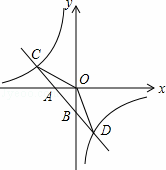
如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=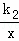 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数y2=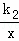 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
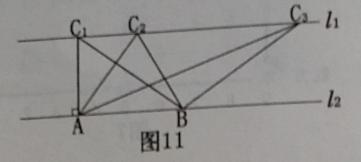
如图11,已知, l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上,设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列是某校教学活动小组学生的年龄情况:13,15,15,16,13,15,14,15(单位:岁).这组数据的中位数和极差分别是( )
A. 15,3 B. 14,15 C. 16,16 D. 14,3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com