练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    因式分解：=     



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    等腰△ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE，则∠EBC的度数为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3，表示的点在数轴上表示时，所在哪两个字母之间（　　）

    A．C与D      B．A与B      C．A与C      D．B与C

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    )如图13，已知Rt△ACB中，∠C＝90°，∠BAC＝45°．

                            

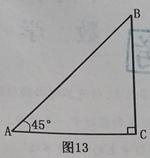
    （1）（4分）用尺规作图，：在CA的延长线上截取AD＝AB，并连接

    BD（不写作法，保留作图痕迹）

    （2）（4分）求∠BDC的度数．

    （3）（4分）定义：在直角三角形中，一个锐角A的邻边与对边的比叫

    做∠A的余切，记作cotA，即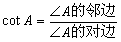，根据定义，利

    用图形求cot22.5°的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     化简的结果是

    A.          B.            C.           D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


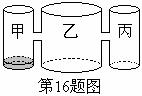    实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1:2:1，，用两个相同的管子在容器的5cm高度处连通（即管子底端离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图所示。若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升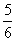cm。

    （1）开始注水1分钟，丙的水位上升＿＿＿cm。

    （2）开始注入     分钟的水量后，乙水位比甲高0.5cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某校规划在一块长AD为18m，宽AB为13m的长方形场地ABCD上，设计分别与AD，AB平行的横向通道和纵向通道，其余部分铺上草皮。

    （1）如图1，若设计三条通道，一条横向，两条纵向，且它们的宽度相等，其余六块草坪相同，其中一块草坪两边之比AM:AN=8:9，问通道的宽是多少？

    （2）为了建造花坛，要修改（1）中的方案，如图2，将三条通道改为两条通道，纵向的宽度改为横向宽度的2倍，其余四块草坪相同，且每一块草坪均有一边长为8m，这样能在这些草坪建造花坛。如图3，在草坪RPCQ中，已知RE⊥PQ于点E，CF⊥PQ于点F，求花坛RECF的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


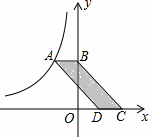
    如图，点A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点C、D在x轴上，且BC∥AD，四边形ABCD的面积为3，则这个反比例函数的解析式为　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


      一组数据：2，3，6，6，7，8，8，8的中位数是（　　）

    　  A．  6  B．  6.5  C．  7  D．  8

    查看答案和解析>>

    同步练习册答案