
阅读下列材料:
问题:在平面直角坐标系 中,一张矩形纸片OBCD按图1所示放置。已知OB=10,BC=6,
中,一张矩形纸片OBCD按图1所示放置。已知OB=10,BC=6,
将这张纸片折叠,使点O落在边CD上,记作点A,折痕与边OD(含端点)交于点E,与边OB(含端点)或其延长线交于点F,求点A的坐标.
小明在解决这个问题时发现:要求点A的坐标,只要求出线段AD的长即可,连接OA,设折痕EF所在直线对应的函数表达式为: ,于是有
,于是有 ,所以在Rt△EOF中,得到
,所以在Rt△EOF中,得到 ,在Rt△AOD中,利用等角的三角函数值相等,就可以求出线段DA的长(如图1)
,在Rt△AOD中,利用等角的三角函数值相等,就可以求出线段DA的长(如图1)

请回答:
(1)如图1,若点E的坐标为 ,直接写出点A的坐标;
,直接写出点A的坐标;
(2)在图2中,已知点O落在边CD上的点A处,请画出折痕所在的直线EF(要求:尺规作图,保留作图痕迹,不写做法);
参考小明的做法,解决以下问题:
(3)将矩形沿直线 折叠,求点A的坐标;
折叠,求点A的坐标;
(4)将矩形沿直线 折叠,点F在边OB上(含端点),直接写出
折叠,点F在边OB上(含端点),直接写出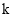 的取值范围.
的取值范围.
(1) ;(2)作图见解析;(3)(3,6);(4)
;(2)作图见解析;(3)(3,6);(4) .
.
【解析】
试题分析:(1)根据矩形和折叠的性质以及勾股定理求解即可.
(2)作AD的垂直平分线交OD于点E,交OB于点F,连接EF,EF即为所求.
(3)过点F作FG⊥DC于点G,通过证明△AEF≌△OEF和△DAE∽△GFAF,根据全等三角形和相似三角形的性质求解.
(4)由于题意中,与k有关的是tan∠AOD,即与Rt△AOD有关,所以我们求解k的取值范围可以转化为求DA的长度的范围.
试题解析:(1)∵根据矩形和折叠的性质,AE=OE=4,DE=2,
∴根据勾股定理,得 .
.
∴ .
.
(2)作图如下:

(3)如图,过点F作FG⊥DC于点G,
∵EF的解析式为 ,
,
∴ .∴OE=n,OF=2n.
.∴OE=n,OF=2n.
∵△AEF≌△OEF,∴AE=OE=n,AF=OF=2n.
∵点A在DC上,且∠EAF=900,∴∠1+∠2=900.
又∵∠2+∠3==900,∴∠1=∠2.
∴△DAE∽△GFAF.∴ .
.
又∵FG=CB=6,∴ .∴DA=3.
.∴DA=3.
∴点A的坐标为(3,6).

(4)如图,过点F作FG⊥DC于点G,
∵EF的解析式为 ,
,
∴ .∴OE=n,OF=
.∴OE=n,OF= .
.
∵△AEF≌△OEF,∴AE=OE=n,AF=OF= .
.
∵点A在DC上,且∠EAF=900,∴∠1+∠2=900.
又∵∠2+∠3==900,∴∠1=∠2.
∴△DAE∽△GFAF.∴ .
.
又∵FG=CB=6,∴ .∴DA=
.∴DA= .
.
当DA最小时,点F与点B重合,此时AF=OB=10,BC=6,得AC=8,DA=2,即 ;
;
当DA最大时,DA=OD=6,即 .
.
∴ .
.
考点:1.阅读理解型的实践操作题;2.折叠问题;3.矩形的性质;4.勾股定理;5.全相似三角形的判定和性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(内蒙古包头、乌兰察布卷)数学(解析版) 题型:选择题
下列计算正确的是( )
A.(﹣1)﹣1=1 B.(﹣1)0=0 C.|﹣1|=﹣1 D.﹣(﹣1)2=﹣1
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市通州区中考二模数学试卷(解析版) 题型:选择题
小美同学在“百度”搜索引擎中输入“中国梦,我的梦”,能搜到与之相关的结果的条数约为9 930 000,这个数用科学记数法表示为( )
A.9.93×105 B.9.93×106 C.99.3×105 D.0.993×107
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
列方程(组)解应用题:
某校甲、乙给贫困地区捐款购买图书,每班捐款总数均为1200元,已知甲班比乙班多8人,乙班人均
捐款是甲班人均捐款的 倍,求:甲、乙两班各有多少名学生.
倍,求:甲、乙两班各有多少名学生.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:解答题
在“母亲节”到来之际,某校九年级团支部组织全体团员到敬老院慰问.为筹集慰问金,团员们利用课余期间去卖鲜花.已知团员们从花店按每 支1.5元的价格买进鲜花共 支,并按每支5元的价格全部卖出,若从花店购买鲜花的同时,还用去50元购买包装材料.
支,并按每支5元的价格全部卖出,若从花店购买鲜花的同时,还用去50元购买包装材料.
(1)求所筹集的慰问金y(元)与x(支)之间的函数表达式;
(2)若要筹集不少于650元的慰问金,则至少要卖出鲜花多少支?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com