列方程（组）解应用题：
某校甲、乙给贫困地区捐款购买图书，每班捐款总数均为1200元，已知甲班比乙班多8人，乙班人均
捐款是甲班人均捐款的
倍，求：甲、乙两班各有多少名学生.
科目：初中数学 来源：2014年初中毕业升学考试（内蒙古呼和浩特卷）数学（解析版） 题型：填空题
某校五个绿化小组一天的植树的棵数如下：10，10，12，x，8． 已知这组数据的平均数是10，那么这组数据的方差是 ．
查看答案和解析>>
科目：初中数学 来源：2013-2014学年北京市通州区中考二模数学试卷（解析版） 题型：解答题
如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF＝∠ABC．
（1）求证：AB＝AC；
（2）若AD＝4，cos∠ABF＝
，求DE的长．
查看答案和解析>>
科目：初中数学 来源：2013-2014学年北京市西城区中考一模数学试卷（解析版） 题型：解答题
阅读下列材料：
问题：在平面直角坐标系
中，一张矩形纸片OBCD按图1所示放置。已知OB=10，BC=6，
将这张纸片折叠，使点O落在边CD上，记作点A，折痕与边OD（含端点）交于点E，与边OB（含端点）或其延长线交于点F，求点A的坐标.
小明在解决这个问题时发现：要求点A的坐标，只要求出线段AD的长即可，连接OA，设折痕EF所在直线对应的函数表达式为：
，于是有
，所以在Rt△EOF中，得到
，在Rt△AOD中，利用等角的三角函数值相等，就可以求出线段DA的长（如图1）
请回答：
（1）如图1，若点E的坐标为
，直接写出点A的坐标；
（2）在图2中，已知点O落在边CD上的点A处，请画出折痕所在的直线EF（要求：尺规作图，保留作图痕迹，不写做法）；
参考小明的做法，解决以下问题：
（3）将矩形沿直线
折叠，求点A的坐标；
（4）将矩形沿直线
折叠，点F在边OB上（含端点），直接写出
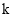的取值范围.
查看答案和解析>>
科目：初中数学 来源：2013-2014学年北京市西城区中考一模数学试卷（解析版） 题型：填空题
如图，在平面直角坐标系
中，点A(1,0)，B(2,0)，正六边形ABCDEF沿x轴正方向无滑动滚动，当点D第一次落在x轴上时，点D的坐标为： ；在运动过程中，点A的纵坐标的最大值是 ；保持上述运动过程，经过
的正六边形的顶点是 .
查看答案和解析>>
科目：初中数学 来源：2013-2014学年北京市燕山区中考一模数学试卷（解析版） 题型：填空题
如图，在平面直角坐标系中，已知点P0坐标为（1，0），将线段OP0绕点O顺时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；将线段OP1绕点O顺时针方向旋转45°，再将其长度伸长为OP1的2倍，得到线段OP2，…，这样依次得到线段OP3，OP4，…，OPn．则点P2的坐标为 ；
当n=4m+1（m为自然数）时，点Pn的坐标为 ．
查看答案和解析>>
科目：初中数学 来源：2013-2014学年北京市朝阳区中考一模数学试卷（解析版） 题型：解答题
如图，CA、CB为⊙O的切线，切点分别为A、B．直径延长AD与CB的延长线交于点E．AB、CO交于点M，连接OB．
（1）求证：∠ABO=
∠ACB；
（2）若sin∠EAB=
，CB=12，求⊙O 的半径及
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
