
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E.AB、CO交于点M,连接OB.
(1)求证:∠ABO= ∠ACB;
∠ACB;
(2)若sin∠EAB= ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及 的值.
的值.

(1)证明见解析;(2)4, .
.
【解析】
试题分析:(1)证明∠ABO =∠BCO即可证得∠ABO= ∠ACB.
∠ACB.
(2)由sin∠BCO =sin∠EAB= 可求得
可求得 =
= ,从而由CB=12求得⊙O 的半径OB为4;由△OBE∽△CAE列比例式得
,从而由CB=12求得⊙O 的半径OB为4;由△OBE∽△CAE列比例式得 =
= .
.
(1)∵CA、CB为⊙O的切线,
∴ CA=CB, ∠BCO= ∠ACB,∴∠CBO=90°.∴ CO⊥AB.
∠ACB,∴∠CBO=90°.∴ CO⊥AB.
∴ ∠ABO +∠CBM=∠BCO +∠CBM=90°.∴ ∠ABO =∠BCO.∴ ∠ABO= ∠ACB.
∠ACB.
(2) ∵ OA=OB, ∴∠EAB=∠ABO.∴ ∠BCO=∠EAB.
∵ sin∠BCO =sin∠EAB= ,∴
,∴  =
= .
.
∵ CB=12,∴ OB=4, 即⊙O 的半径为4.
∵∠OBE=∠CAE=90°,∠E=∠E,∴△OBE∽△CAE.∴ =
= .
.
∵CA=CB=12,∴ =
= .
.
考点:1.切线的性质;2.等腰三角形的性质;3锐角三角函数定义;4.勾股定理;5.相似三角形的判定和性质.


科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
列方程(组)解应用题:
某校甲、乙给贫困地区捐款购买图书,每班捐款总数均为1200元,已知甲班比乙班多8人,乙班人均
捐款是甲班人均捐款的 倍,求:甲、乙两班各有多少名学生.
倍,求:甲、乙两班各有多少名学生.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:解答题
对于平面直角坐标系 xOy中的点P(a,b),若点 的坐标为(
的坐标为( ,
, )(其中k为常数,且
)(其中k为常数,且 ),则称点
),则称点 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为 (1+
(1+ ,
, ),即
),即 (3,6).
(3,6).
(1)①点P 的“2属派生点”
的“2属派生点”  的坐标为____________;
的坐标为____________;
②若点P的“k属派生点” 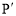 的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
(2)若点P在x轴的正半轴上,点P的“k属派生点”为 点,且△
点,且△ 为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________;
(3)如图, 点Q的坐标为(0, ),点A在函数
),点A在函数 的图象上,且点A是点B的“
的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:选择题
如图,点P是以O为圆心, AB为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P重合, 当此三角板绕点P旋转时,它的斜边和直角边所在的直线与直径AB分别相交于C、D两点.设线段AD的长为x,线段BC的长为y,则下列图象中,能表示y与x的函数关系的图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:解答题
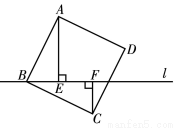
如图,四边形ABCD是正方形,AE、CF分别垂直于过顶点B的直线l,垂足分别为E、F.
求证:BE=CF.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:填空题
请写出一个经过第一、二、三象限,并且与y轴交与点(0,1)的直线表达式 ____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com