
对于平面直角坐标系 xOy中的点P(a,b),若点 的坐标为(
的坐标为( ,
, )(其中k为常数,且
)(其中k为常数,且 ),则称点
),则称点 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为 (1+
(1+ ,
, ),即
),即 (3,6).
(3,6).
(1)①点P 的“2属派生点”
的“2属派生点”  的坐标为____________;
的坐标为____________;
②若点P的“k属派生点” 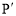 的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
(2)若点P在x轴的正半轴上,点P的“k属派生点”为 点,且△
点,且△ 为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________;
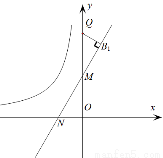
(3)如图, 点Q的坐标为(0, ),点A在函数
),点A在函数 的图象上,且点A是点B的“
的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.

(1)①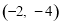 ;②(1,2)(答案不唯一);(2)
;②(1,2)(答案不唯一);(2)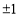 ;(3)
;(3)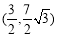 .
.
【解析】
试题分析:(1)①根据派生点的定义,点P 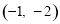 的“2属派生点”
的“2属派生点” 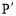 的坐标为(
的坐标为( ,
,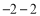 ),即
),即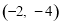 .
.
②答案不唯一,只需横、纵坐标之和为3即可,如(1,2).
(2)若点P在x轴的正半轴上,则P(a,0),点P的“k属派生点”为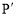 点为(
点为( ,
,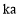 ).
).
∵且△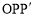 为等腰直角三角形,∴
为等腰直角三角形,∴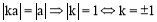 .
.
(3)求出点B所在的直线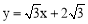 ,根据垂直线段最短的性质即可求得B点坐标.
,根据垂直线段最短的性质即可求得B点坐标.
试题解析:(1)① .
.
②.(1,2).
(2)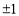 .
.
(3)设B(a,b).
∵B的“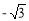 属派生点”是A,∴
属派生点”是A,∴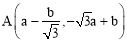 .
.
∵点A还在反比例函数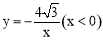 的图象上,
的图象上,
∴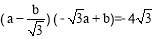 .∴
.∴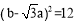 .
.
∵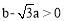 ,∴
,∴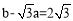 .∴
.∴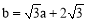 .
.
∴B在直线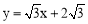 上.
上.
过Q作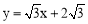 的垂线QB1,垂足为B1,
的垂线QB1,垂足为B1,
∵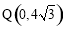 ,且线段BQ最短,∴B1即为所求的点B.
,且线段BQ最短,∴B1即为所求的点B.
∴易求得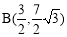 .
.
考点:1.新定义;2.开放型;3.等腰直角三角形的性质;4.曲线上点的坐标与方程的关系;5.垂直线段最短的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2013-2014学年北京市通州区中考二模数学试卷(解析版) 题型:解答题
如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.
(1)求证:AB=AC;
(2)若AD=4,cos∠ABF= ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,已知点P0坐标为(1,0),将线段OP0绕点O顺时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;将线段OP1绕点O顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2,…,这样依次得到线段OP3,OP4,…,OPn.则点P2的坐标为 ;
当n=4m+1(m为自然数)时,点Pn的坐标为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:选择题
如图所示,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为( )

A.20° B.70° C .100° D.110°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:解答题
社会消费品通常按类别分为:吃类商品、穿类商品、用类商品、烧类商品,其零售总额是反映居民生活水平的一项重要数据.为了了解北京市居民近几年的生活水平,小红参考北京统计信息网的相关数据绘制了统计图的一部分:

(1)北京市2013年吃类商品的零售总额占社会消费品零售总额的百分比为 ;
(2)北京市2013年吃类商品零售总额约为1673亿元,那么当年的社会消费品零售总额约为 亿元;请补全条形统计图,并标明相应的数据;
(3)小红根据条形统计图中的数据,绘制了北京市2010至2013年社会消费品零售总额年增长率统计表(如下表),其中2013年的年增长率为 (精确到1%);请你估算,如果按照2013年的年增长率持续增长,当年社会消费品零售总额超过10000亿元时,最早要到 年(填写年份).
北京市2010至2013年社会消费品零售总额年增长率统计表 | ||||
| 2010年 | 2011年 | 2012年 | 2013年 |
年增长率(精确到1%) | 17% | 11% | 12% |
|
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:解答题
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E.AB、CO交于点M,连接OB.
(1)求证:∠ABO= ∠ACB;
∠ACB;
(2)若sin∠EAB= ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com