
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 +7x2y2)÷(-7x2y)=
+7x2y2)÷(-7x2y)= +5xy-y.你能复原被污染的地方吗?请你试一试.
+5xy-y.你能复原被污染的地方吗?请你试一试.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
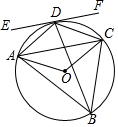 如图,⊙O是△ABC的外接圆,连接OA,OC,BD平分∠ABC,交⊙O于点D,连接AD,CD,过点D作直线EF∥AC,已知∠BDC+∠ACB=130°.
如图,⊙O是△ABC的外接圆,连接OA,OC,BD平分∠ABC,交⊙O于点D,连接AD,CD,过点D作直线EF∥AC,已知∠BDC+∠ACB=130°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
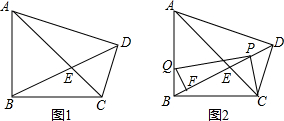
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com