在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在（ ）
A． 第一象限 B． 第二象限 C． 第三象限 D． 第四象限
名校课堂系列答案科目：初中数学 来源： 题型：
已知反比例函数y=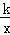
的图象经过点（3，2），那么下列四个点中，也在这个函数图象上的是（ ）
A． （3，﹣2） B． （﹣2，﹣3） C． （1，﹣6） D． （﹣6，1）
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）的顶点为B（2，1），且过点A（0，2），直线y=x与抛物线交于点D，E（点E在对称轴的右侧），抛物线的对称轴交直线y=x于点C，交x轴于点G，EF⊥x轴，垂足为F，点P在抛物线上，且位于对称轴的右侧，PQ⊥x轴，垂足为点Q，△PCQ为等边三角形
（1）求该抛物线的解析式；
（2）求点P的坐标；
（3）求证：CE=EF；
（4）连接PE，在x轴上点Q的右侧是否存在一点M，使△CQM与△CPE全等？若存在，试求出点M的坐标；若不存在，请说明理由．[注：3+2
=（+1）2]．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP=4，则线段OM的最小值是（ ）
A． 0 B． 1 C． 2 D． 3
查看答案和解析>>
科目：初中数学 来源： 题型：
在一次定点投篮训练中，五位同学投中的个数分别为3，4，4，6，8，则关于这组数据的说法不正确的是（ ）
A．平均数是5 
B．中位数是6 C．众数是4 D．方差是3.2
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．
（1）求证：四边形DEFG为菱形；
（2）若CD=8，CF=4，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
÷（a﹣
），其中a，b满足|a﹣3|+（b﹣2）2=0．