
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0,2),直线y=x与抛物线交于点D,E(点E在对称轴的右侧),抛物线的对称轴交直线y=x于点C,交x轴于点G,EF⊥x轴,垂足为F,点P在抛物线上,且位于对称轴的右侧,PQ⊥x轴,垂足为点Q,△PCQ为等边三角形

(1)求该抛物线的解析式;
(2)求点P的坐标;
(3)求证:CE=EF;
(4)连接PE,在x轴上点Q的右侧是否存在一点M,使△CQM与△CPE全等?若存在,试求出点M的坐标;若不存在,请说明理由.[注:3+2 =(
=( +1)2].
+1)2].
解:(1)设抛物线的表达式为y=a(x﹣2)2+1,将点A(0,2)代入,得a(0﹣2)2+1=2,
解这个方程,得a=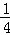 ,
,
∴抛物线的表达式为y=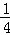 (x﹣2)2+1=
(x﹣2)2+1=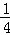 x2﹣x+2;
x2﹣x+2;
(2)将x=2代入y=x,得y=2
∴点C的坐标为(2,2)即CG=2,
∵△PCQ为等边三角形
∴∠CQP=60°,CQ=PQ,
∵PQ⊥x轴,
∴∠CQG=30°,
∴CQ=4,GQ=2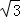 .
.
∴OQ=2+2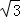 ,PQ=4,
,PQ=4,
将y=4代入y=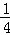 (x﹣2)2+1,得4=
(x﹣2)2+1,得4=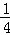 (x﹣2)2+1
(x﹣2)2+1
解这个方程,得x1=2+2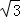 =OQ,x2=2﹣2
=OQ,x2=2﹣2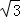 <0(不合题意,舍去).
<0(不合题意,舍去).
∴点P的坐标为(2+2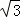 ,4);
,4);
(3)把y=x代入y=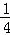 x2﹣x+2,得x=
x2﹣x+2,得x=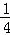 x2﹣x+2
x2﹣x+2
解这个方程,得x1=4+2 ,x2=4﹣2
,x2=4﹣2 <2(不合题意,舍去)
<2(不合题意,舍去)
∴y=4+2 =EF
=EF
∴点E的坐标为(4+2 ,4+2
,4+2 )
)
∴OE=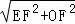 =4+4
=4+4 ,
,
又∵OC=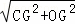 =2
=2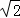 ,
,
∴CE=OE﹣OC=4+2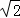 ,
,
∴CE=EF;
(4)不存在.
如图,假设x轴上存在一点,使△CQM≌△CPE,则CM=CE,∠QCM=∠PCE
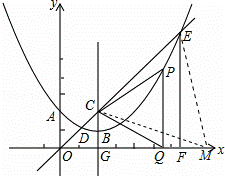
∵∠QCP=60°,
∴∠MCE=60°
又∵CE=EF,
∴EM=EF,
又∵点E为直线y=x上的点,
∴∠CEF=45°,
∴ 点M与点F不重合.
点M与点F不重合.
∵EF⊥x轴,这与“垂线段最短”矛盾,
∴原假设错误,满足条件的点M不存在.


科目:初中数学 来源: 题型:
某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= ;⑤S四边形CDEF=
;⑤S四边形CDEF= S△ABF,其中正确的结论有( )
S△ABF,其中正确的结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com