
某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.
解:(1)设甲种材料每千克x元,乙种材料每千克y元,
依题意得: ,
,
解得: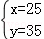 ;
;
答:甲种材料每千克25元,乙种材料每千克35元.
(2)设生产B产品a件,生产A产品(60﹣a)件.
依题意得: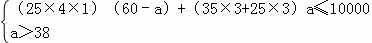 ,
,
解得:38<a≤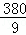 ;
;
∵a的值为非负整数,
∴a=39、40、41、42;
答:共有如下四种方案:
A(件) 21 20 19 18
B(件) 39 40 41 42
(3)生产A产品21件,B产品39件成本最低.理由如下:
设生产成本为W元,则W与a的关系式为:
W=(25×4+35×1+40)(60﹣a)+(35×3+25×3+50)a=55a+10 500,
即W是a的一次函数,
∵k=55>0
∴W随a增大而增大
∴当a=39时,总成本最低;
即生产A产品21件,B产品39件成本最低.


科目:初中数学 来源: 题型:
黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
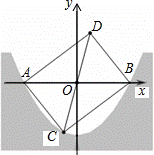
某水渠的横截面呈抛物线形,现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.已知水面的宽AB=8米,且抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,求点C关于原点O的对称点D;
(3)写出四边形ACBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=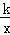 的图象经过点(3,2),那么下列四个点中,也在这个函数图象上的是( )
的图象经过点(3,2),那么下列四个点中,也在这个函数图象上的是( )
A. (3,﹣2) B. (﹣2,﹣3) C. (1,﹣6) D. (﹣6,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0,2),直线y=x与抛物线交于点D,E(点E在对称轴的右侧),抛物线的对称轴交直线y=x于点C,交x轴于点G,EF⊥x轴,垂足为F,点P在抛物线上,且位于对称轴的右侧,PQ⊥x轴,垂足为点Q,△PCQ为等边三角形

(1)求该抛物线的解析式;
(2)求点P的坐标;
(3)求证:CE=EF;
(4)连接PE,在x轴上点Q的右侧是否存在一点M,使△CQM与△CPE全等?若存在,试求出点M的坐标;若不存在,请说明理由.[注:3+2 =(
=( +1)2].
+1)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com