
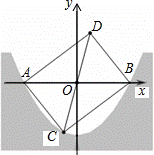
某水渠的横截面呈抛物线形,现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.已知水面的宽AB=8米,且抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,求点C关于原点O的对称点D;
(3)写出四边形ACBD的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知:如图,直线y=mx+n与抛物线 交于点A(1,0)和点B,与抛物线的对称轴x=﹣2交于点C(﹣2,4),直线f过抛物线与x轴的另一个交点D且与x轴垂直.
交于点A(1,0)和点B,与抛物线的对称轴x=﹣2交于点C(﹣2,4),直线f过抛物线与x轴的另一个交点D且与x轴垂直.
(1)求直线y=mx+n和抛物线 的解析式;
的解析式;
(2)在直线f上是否存在点P,使⊙P与直线y=mx+n和直线x=﹣2都相切.若存在,求出圆心P的坐标,若不存在,请说明理由;
(3)在线段AB上有一个动点M(不与点A、B重合),过点M作x轴的垂线交抛物线于点N,当MN的长为多少时,△ABN的面积最大,请求出这个最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
按要求化简:(a﹣1)÷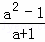 •
•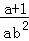 ,并选择你喜欢的整数a,b代入求值.
,并选择你喜欢的整数a,b代入求值.
小聪计算这一题的过程如下:
解:原式=(a﹣1)÷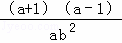 …①
…①
=(a﹣1)•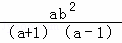 …②
…②
=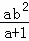 …③
…③
当a=1,b=1时,原式=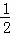 …④
…④
以上过程有两处关键性错误,第一次出错在第 步(填序号),原因: ;
还有第 步出错(填序号),原因: .
请你写出此题的正确解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xoy中,已知点A(2,1)、B(﹣1,1)、C(﹣1,﹣3)、D(2,﹣3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为

查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com