
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 增减 | +10 | -4 | -8 | +22 | -20 |
分析 (1)用标准加上10即可求解;
(2)计算产量最多的一天与产量最少的一天的差即可;
(3)根据题意求和,再进行计算即可.
解答 解:(1)2000+10=2010(个).
答:根据记录可知这一周第一天生产2010个配件;
(2)22-(-20)=42(个).
答:这一周产量最多的一天比产量最少的一天多生产42个配件;
(3)15×(2000×5+10-4-8+22-20)×52
=15×10000×52
=7800000
=7.8×106(元).
答:该周产量估计该工厂生产这种型号的配件的年产值是7.8×106元.
故答案为:2010;42.
点评 本题考查的是正负数在实际生活中的应用,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量并根据题意进行有理数的加减运算.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
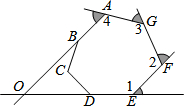 如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为40°.
如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com