
分析 设去年每吨水费为x元,则今年每吨水费为(1+$\frac{1}{3}$)x元,小丽家去年12月的用水量为$\frac{15}{x}$吨,今年2月的用水量为($\frac{15}{x}$+5)吨,根据应缴水费=水费单价×用水量即可得出关于x的分式方程,解之经检验后即可得出x值,将其代入(1+$\frac{1}{3}$)x中即可得出结论.
解答 解:设去年每吨水费为x元,则今年每吨水费为(1+$\frac{1}{3}$)x元,小丽家去年12月的用水量为$\frac{15}{x}$吨,今年2月的用水量为($\frac{15}{x}$+5)吨,
根据题意得:($\frac{15}{x}$+5)(1+$\frac{1}{3}$)x=30,
解得:x=1.5,
经检验得:x=1.5是原方程的根,
∴(1+$\frac{1}{3}$)x=2.
答:该市今年居民用水的价格为2元/吨.
点评 本题考查了分式方程的应用,根据应缴水费=水费单价×用水量列出关于x的分式方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
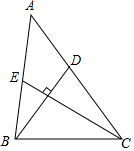 如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE,若BD=4,CE=6,则△ABC的面积为( )
如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE,若BD=4,CE=6,则△ABC的面积为( )| A. | 12 | B. | 24 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{3}{x}$ | B. | y=$\frac{x}{3}$ | C. | y=$\frac{1}{2x}$ | D. | xy=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com